Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
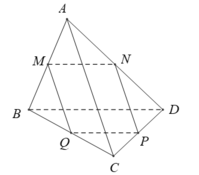
- Vì MN, PQ lần lượt là đường trung bình tam giác ABD, BCD nên:
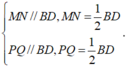
- Nên MN // PQ, MN = PQ.
⇒ tứ giác MNPQ là hình bình hành.
- Do đó MP và NQ cùng thuộc mặt phẳng MNPQ và hai đường thẳng này cắt nhau.

Trong mặt phẳng (ACD) : FN cắt CD tại H ⇒ H ∈ (EFG) và H ∈ (BCD) ⇒ H ∈ MG là giao tuyến của (EFG) và (BCD) hay FN, MG, CD đồng quy tại H ⇒ M, N, F, G đồng phẳng
Đáp án D

Đáp án B
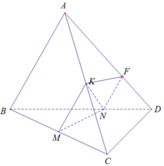
Xét (MNK) và (ABD) có:
N là điểm chung
AB // MK ⇒ A B ⫽ M N K
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua N và song song AB
d cắt AB tại điểm F cần tìm
Vì FN // AB ( cách dựng)
![]()

Ta có:
\(\left. \begin{array}{l}J \in C{\rm{D}}\\C{\rm{D}} \subset \left( {IC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {IC{\rm{D}}} \right)\).
Vậy bốn điểm \(I,J,C,D\) đồng phẳng.
Chọn D.

Đáp án D
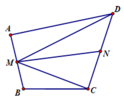
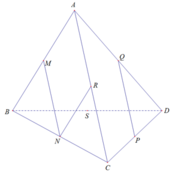
+ Trong tam giác CAD có S và N lần lượt là trung điểm của AC và CD
Suy ra SN là đường trung bình của tam giác CAD
SN // AD (1)
Tương tự MR cũng là đường trung bình của tam giác ABD
MR // AD (2)
Từ (1) và (2) suy ra: SN // MR nên đáp án A đúng
Chứng minh tương tự ta cũng có: SM // NR (//BC)
Do đó tứ giác MRNS là hình bình hành nên đáp án C đúng.
Suy ra hai đường chéo SR và MN cắt nhau tại G với G là trung điểm của mỗi đường chéo.
Lại có: NQ // MP (//AC) và MQ // NP (//BD)
Suy ra tứ giác MQNP là hình bình hành
Suy ra hai đường chéo QP và MN cắt nhau tại trung điểm của mỗi đường
Mà G là trung điểm của MN
Do đó G cũng là trung điểm của QP
Vậy ba đường thẳng MN, PQ, SR đồng quy tại G.
Đáp án B đúng
Đáp án D sai vì P và Q cùng thuộc một mặt phẳng với M và N nhưng không cùng thuộc một mặt phẳng với hai điểm S và R.
Chọn đáp án D

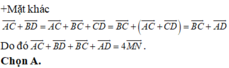
Đáp án D