


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





a) Vì I là trọng tâm của tam giác ABD nên \(AI=\dfrac{1}{3}AC\)


?o?n th?ng a: ?o?n th?ng [A, D] ?o?n th?ng b: ?o?n th?ng [A, B] ?o?n th?ng e: ?o?n th?ng [B, C] ?o?n th?ng f: ?o?n th?ng [C, D] ?o?n th?ng g: ?o?n th?ng [A, C] ?o?n th?ng i: ?o?n th?ng [S, H] ?o?n th?ng j: ?o?n th?ng [S, A] ?o?n th?ng k: ?o?n th?ng [S, B] ?o?n th?ng l: ?o?n th?ng [S, C] ?o?n th?ng m: ?o?n th?ng [S, D] ?o?n th?ng n: ?o?n th?ng [M, C] ?o?n th?ng p: ?o?n th?ng [M, B] ?o?n th?ng p: ?o?n th?ng [M, B] A = (-1.48, 1.8) A = (-1.48, 1.8) A = (-1.48, 1.8) D = (2.3, 1.8) D = (2.3, 1.8) D = (2.3, 1.8) B = (-3.12, -0.08) B = (-3.12, -0.08) B = (-3.12, -0.08) ?i?m C: Giao ?i?m c?a c, d ?i?m C: Giao ?i?m c?a c, d ?i?m C: Giao ?i?m c?a c, d ?i?m H: (3A + C) / 4 ?i?m H: (3A + C) / 4 ?i?m H: (3A + C) / 4 ?i?m S: ?i?m tr�n h ?i?m S: ?i?m tr�n h ?i?m S: ?i?m tr�n h ?i?m M: (S + A) / 2 ?i?m M: (S + A) / 2 ?i?m M: (S + A) / 2
Do CM là trung tuyến của SAC nên M là trung điểm SA.
\(\dfrac{V_{SMBC}}{V_{SABC}}=\dfrac{SM}{SA}=\dfrac{1}{2}\)
Ta có \(AC=\sqrt{AB^2+AC^2}=a\sqrt{2}\) nên \(AH=\dfrac{1}{4}AC=\dfrac{a\sqrt{2}}{4}\)
Suy ra \(SH=\sqrt{SA^2-AH^2}=\sqrt{a^2-\dfrac{2a^2}{16}}=\dfrac{a\sqrt{14}}{4}\)
Do đó \(V_{SABC}=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{a\sqrt{14}}{4}.\dfrac{a^2}{2}=\dfrac{a^3\sqrt{14}}{24}\)
Vậy \(V_{SMBC}=\dfrac{1}{2}V_{SABC}=\dfrac{a^3\sqrt{14}}{48}\)


\(V_{ABSI}=V_{S.ABI}=\dfrac{1}{2}V_{S.ABCD}=\dfrac{a^3}{9}\)

Ta có \(\left(SHC\right)\cap\left(SHD\right)=SH\)
Từ giả thiết \(\left(SHC\right)\perp\left(ABCD\right);\left(SHD\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(\Leftrightarrow V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}AB.AD.SH=\frac{1}{3}a^2\sqrt{3}.SH\left(1\right)\)
Ta có \(SH\perp\left(ABCD\right)\Rightarrow HD\) là hình chiếu của SD trên (ABCD), suy ra góc giữa SD và (ABCD) là \(\widehat{SDH}=60^0\Rightarrow SH=HD\tan\widehat{SDHH}=\frac{a\sqrt{39}}{2}\)
Khi đó \(V_{S.ABCD}=\frac{1}{2}a^3\sqrt{13}\)
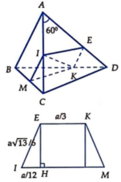
Dựng hình bình hành ACBE. Khi đó AC//BE suy ra AC//(SBE)
\(\Rightarrow d\left(AC,SB\right)=d\left(AC,\left(SBE\right)\right)=d\left(A,\left(SBE\right)\right)=2d\left(H,\left(SBE\right)\right)\)
Gọi K, I lần lượt là hình chiếu của H trên BE và SK.
Khi đó \(BE\perp KH,BE\perp SH\Rightarrow BE\perp HI\left(1\right)\)
Mặt khác \(HI\perp SK\left(2\right)\)
Từ (1) và (2) suy ra \(HI\perp\left(SBE\right)\Rightarrow d\left(H,\left(SBE\right)\right)=HI\)
Tính được \(HK=\frac{a\sqrt{3}}{4};HI=\frac{a\sqrt{39}}{\sqrt{212}}\)
\(\Rightarrow d\left(AC,SB\right)=2d\left(H,\left(SBE\right)\right)=2HI=\frac{a\sqrt{39}}{\sqrt{53}}=\frac{a\sqrt{2067}}{53}\)

A C D B (P) (Q)
Do \(\left(P\right)\perp\left(Q\right)\) và \(\left(P\right)\cap\left(Q\right)=\Delta\)
và \(DB\perp\left(\Delta\right)\left(DB\in\left(Q\right)\right)\)
Nên \(DB\perp\left(P\right)\Rightarrow DB\perp BC\)
Tương tự ta có :
\(CA\perp AD\)
Vì \(\widehat{CAD}=\widehat{DBC}=90^0\) nên CD chính là đường kính hình cầu ngoại tiếp tứ diện ABCD.
Gọi R là bán kính của hinh cầu này thì :
\(R=\frac{1}{2}CD\) (1)
Theo định lý Pitagoc trong 2 tam giác vuông CAD, ABD ta có :
\(CD^2=CA^2+AD^2=CA^2+BA^2+BD^2=3a^2\)
\(\Rightarrow CD=a\sqrt{3}\) (2)
Từ (1) và (2) suy ra \(R=\frac{a\sqrt{3}}{2}\)

Qua O vẽ đường thẳng d vuông góc với (ABCD)
Khi đó d là trục đường tròn ngoại tiếp hình vuông ABCD
Gọi H là trung điểm của cạnh SA
Trong mặt phẳng (SAO) đường trung trực của đoạn SA cắt đường thẳng SO tại I , ta có: \(\Delta SAO\) đòng dạng \(\Delta SIH\)
\(\Rightarrow\dfrac{SA}{SO}=\dfrac{SI}{SH}\Leftrightarrow SI=\dfrac{SA.SH}{SO}=\dfrac{SA^2}{2SO}\)
Mà \(SA^2=SO^2+OA^2=\left(\dfrac{a}{2}\right)^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2=\dfrac{3a^2}{4}\)
\(\Leftrightarrow SA=\dfrac{a\sqrt{3}}{2}\)
Khi đó \(SI=\dfrac{3a^2}{\dfrac{4}{2.\dfrac{a}{2}}}=\dfrac{3a}{4}\)
Mặt khác \(\left\{{}\begin{matrix}IS=IA\\IA=IB=IC=ID\end{matrix}\right.\)
\(\Rightarrow IS=IA=IB=IC=ID=\dfrac{3a}{4}\)
Vậy mặt cầu ngoại tiếp hình chóp S.ABCD có tâm là I và bán kính \(R=SI=\dfrac{3a}{4}\)
Diện tích mặt cầu là: \(S=4\pi R^2=4\pi.\left(\dfrac{3a}{4}\right)^2=\dfrac{9\pi\pi^2}{4}\)
Thể tích khối cầu là: \(V=\dfrac{4}{3}\pi R^2=\dfrac{4}{3}\pi.\left(\dfrac{3a}{4}\right)^2=\dfrac{9\pi\pi^2}{16}\)