Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tao có: \(\overrightarrow{BC}.\overrightarrow{AD}=\overrightarrow{BC}\left(\overrightarrow{DC}+\overrightarrow{CA}\right)=\overrightarrow{CB}.\overrightarrow{CD}-\overrightarrow{CB}.\overrightarrow{CA}\)
\(=\frac{1}{2}\left(CB^2+CD^2-BD^2\right)-\frac{1}{2}\left(CB^2+CA^2-AB^2\right)\)
\(=\frac{1}{2}\left(AB^2+CD^2-BD^2-CA^2\right)\)
\(\Rightarrow\cos\left(\overrightarrow{BC},\overrightarrow{DA}\right)=\frac{1}{2}.\frac{c^2+c'^2-b^2-b'^2}{2aa'}\)

Câu 8:
Kẻ \(AH\perp SM\)
Trong mặt phẳng (SBC), qua H kẻ đường thẳng song song BC cắt SB và SC lần lượt tại P và Q
\(\Rightarrow\Delta APQ\) là thiết diện của (P) và chóp
\(AM=\frac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow SA=AM\Rightarrow\Delta SAM\) vuông cân tại A
\(\Rightarrow AH=\frac{SA\sqrt{2}}{2}=\frac{a\sqrt{6}}{4}\) đồng thời H là trung điểm SM
\(\Rightarrow PQ=\frac{1}{2}BC=\frac{a}{2}\) (đường trung bình)
\(\Rightarrow S_{\Delta APQ}=\frac{1}{2}AH.PQ=\frac{a^2\sqrt{6}}{16}\)
Câu 9.
\(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(SH=AH=\frac{a\sqrt{3}}{2}\Rightarrow\Delta SAH\) vuông cân tại H
\(\Rightarrow\widehat{SAH}=45^0\)
Câu 6:
Bạn kiểm tra lại đề, \(SO\perp\left(ABCD\right)\Rightarrow SO\perp OB\Rightarrow\widehat{SOB}=90^0\)
Nên không thể có chuyện \(tan\widehat{SOB}=\frac{1}{2}\)
Câu 7:
H là trực tâm tam giác ABC \(\Rightarrow BH\perp AC\)
Mà \(SA\perp\left(ABC\right)\Rightarrow SA\perp BH\)
\(\Rightarrow BH\perp\left(SAC\right)\Rightarrow BH\perp SC\) (1)
K là trực tâm tam giác SBC \(\Rightarrow BK\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(BHK\right)\Rightarrow\) góc giữa SC và (BHK) bằng 90 độ

1/ \(\overrightarrow{AB}^2-\overrightarrow{AD}^2=\overrightarrow{BC}^2-\overrightarrow{CD}^2\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{AB}-\overrightarrow{AD}\right)=\left(\overrightarrow{BC}+\overrightarrow{CD}\right)\left(\overrightarrow{BC}-\overrightarrow{CD}\right)\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AD}\right).\overrightarrow{DB}=\overrightarrow{BD}\left(\overrightarrow{BC}-\overrightarrow{CD}\right)=\overrightarrow{DB}\left(\overrightarrow{CB}+\overrightarrow{CD}\right)\)
Gọi M là trung điểm BD
\(\Rightarrow2\overrightarrow{AM}.\overrightarrow{DB}=2\overrightarrow{CM}.\overrightarrow{DB}\)
\(\Leftrightarrow\overrightarrow{DB}.\left(\overrightarrow{AM}-\overrightarrow{CM}\right)=0\)
\(\Leftrightarrow\overrightarrow{BD}.\overrightarrow{AC}=0\)
2/ \(A=\left|\overrightarrow{a}-\overrightarrow{b}\right|\Rightarrow A^2=\overrightarrow{a}^2-2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2\)
\(=a^2+b^2-2ab.cos\left(\overrightarrow{a};\overrightarrow{b}\right)=4^2+5^2-2.4.5.cos120^0=61\)
\(\Rightarrow A=\sqrt{61}\)
b/ \(B=\left|2\overrightarrow{a}+\overrightarrow{b}\right|\Rightarrow B^2=4a^2+b^2+4\overrightarrow{a}.\overrightarrow{b}\)
\(=4a^2+b^2+4ab.cos120^0=49\)
\(\Rightarrow B=7\)
3/ \(\left|\overrightarrow{x}\right|=\left|\overrightarrow{a}-2\overrightarrow{b}\right|\Rightarrow\left|\overrightarrow{x}\right|^2=a^2+4b^2-4\overrightarrow{a}.\overrightarrow{b}=12\)
\(\Rightarrow\left|\overrightarrow{x}\right|=2\sqrt{3}\)
\(\left|\overrightarrow{y}\right|^2=a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=5\Rightarrow\left|\overrightarrow{y}\right|=\sqrt{5}\)
\(\overrightarrow{x}.\overrightarrow{y}=\left(\overrightarrow{a}-2\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)=a^2+2b^2-3\overrightarrow{a}.\overrightarrow{b}=4\)
\(\Rightarrow cos\alpha=\frac{\overrightarrow{x}.\overrightarrow{y}}{\left|\overrightarrow{x}\right|.\left|\overrightarrow{y}\right|}=\frac{4}{2\sqrt{15}}=\frac{2\sqrt{15}}{15}\)

a có \(\angle \left(\right. S C , \left(\right. A B C D \left.\right) \left.\right) = 45^{\circ}\).
Nghĩa là hình chiếu của \(S\) xuống đáy nằm trên đường chéo \(B D\).
Xét tam giác cân \(S A B\), do tính đối xứng ⇒ khoảng cách từ \(A\) đến \(\left(\right. S C D \left.\right)\) chính bằng nửa cạnh hình vuông:
\(d\left(\right.A,\left(\right.SCD\left.\right)\left.\right)=\frac{a}{2}\)
Với \(M\) là trung điểm \(S A\), khoảng cách giảm đi một nửa:
\(d\left(\right.M,\left(\right.SCD\left.\right)\left.\right)=\frac{a}{4}\)
Đáp số
\(d \left(\right. A , \left(\right. S C D \left.\right) \left.\right) = \frac{a}{2}\)
\(d \left(\right. M , \left(\right. S C D \left.\right) \left.\right) = \frac{a}{4}\)

11.
\(SA\perp\left(ABCD\right)\Rightarrow\) AC là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(\Rightarrow\widehat{SCA}=\varphi\)
\(AC=BD=\sqrt{AB^2+AD^2}=a\sqrt{13}\)
\(tan\varphi=\frac{SA}{AC}=\frac{\sqrt{13}}{13}\)
12.
Hai vecto \(\overrightarrow{AB}\) và \(\overrightarrow{EF}\) song song cùng chiều
\(\Rightarrow\left(\overrightarrow{AB};\overrightarrow{EG}\right)=\left(\overrightarrow{EF};\overrightarrow{EG}\right)=\widehat{GEF}=45^0\)
8.
Qua O có 1 và chỉ 1 mặt phẳng vuông góc \(\Delta\)
9.
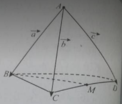
Gọi O là tâm tam giác BCD
\(\Rightarrow AO\perp\left(BCD\right)\Rightarrow AO\perp CD\)
Mà \(CD\perp BO\) (trung tuyến đồng thời là đường cao)
\(\Rightarrow CD\perp\left(ABO\right)\Rightarrow CD\perp AB\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{CD}=0\)
10.
\(AB\perp AD\Rightarrow\widehat{BAD}=90^0\)

s B A D C O M
Hình chiếu vuông góc của SA lên (ABCD) là AO nên góc giữa SA và (ABCD) là \(\widehat{SAO}\)
Xét \(\Delta SAO\left(\perp O\right)\) ta có : \(SA=\frac{a\sqrt{5}}{2};AO=\frac{1}{2}AC=\frac{1}{2}a\sqrt{2}\)
\(\cos\widehat{SAO}=\frac{AO}{SA}=\frac{\frac{a\sqrt{2}}{2}}{\frac{a\sqrt{5}}{2}}=\frac{\sqrt{10}}{5}\)
c. Xét \(\Delta SOC\) có : \(\begin{cases}SO\perp BD\\OC\perp BD\end{cases}\) nên \(\left(SOC\right)\perp BD\) mà \(OM\subset\left(SOC\right)\Rightarrow OM\perp BD\)
xét : \(\left(MBD\right)\cap\left(ABCD\right)=BD\)
Trong (MBD) có \(OM\perp BD\)
Trong (ABCD) có \(OC\perp BD\)
Vậy góc giữa (MBD) và (ABCD) là \(\widehat{MOC}\)
Ta có : \(\Delta SAC\) đồng dạng với \(\Delta MOC\) (vì \(CM=\frac{1}{2}CS;CO=\frac{1}{2}CA\))nên \(\widehat{MOC}=\widehat{SAC}\)
Đáp án A