Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Để giải thích câu trắc nghiệm này, ta cần xem xét vị trí của các điểm M, M', N, N' trên cạnh AB và CD của tứ diện ABCD. Nếu các điểm M, M', N, N' được chọn sao cho MN và M'N' là hai đường thẳng song song, tức là MN // M'N', thì đáp án là D. song song. Nếu các điểm M, M', N, N' được chọn sao cho MN và M'N' là hai đường thẳng chéo nhau, tức là MN và M'N' cắt nhau tại một điểm, thì đáp án là C. chéo nhau.
Tuy nhiên, câu trắc nghiệm không đưa ra thông tin cụ thể về vị trí của các điểm M, M', N, N', nên không thể xác định chính xác đáp án. Do đó, đáp án có thể là B. cắt nhau hoặc song song.
Vì vậy, câu trả lời cuối cùng là B. cắt nhau hoặc song song.
Nghĩ ra hướng làm rồi cơ mà giờ "bỗng dưng bận" nên để lát nữa tui "múa bút" nhó ahehe :3
Mà viết thử hướng làm cho bà nghĩ coi sao.
Phần bài ũy tích thì sẽ chứng minh theo 2 phần là phần đảo và phần thuận
Phần thuân: Có I là trung điểm MN thì chứng minh khi M, N di động thì I sẽ di động trên đường thẳng HK (H là TD AB, K là trung điểm FC)
Phần đảo: Có I thuộc HK, chứng minh tồn tại 2 điểm M thuộc AC, N thuộc BF sao cho AM=BN và nhận I làm trung điểm MN
Đó, nghĩ thử đi đã :3
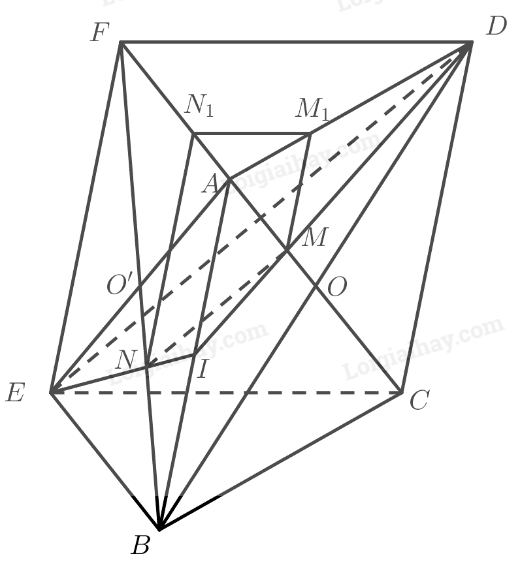
\(\begin{array}{l}\left. \begin{array}{l}N{N_1}\parallel AB \Rightarrow \frac{{A{N_1}}}{{AF}} = \frac{{BN}}{{BF}} = \frac{1}{3}\\M{M_1}\parallel AB \Rightarrow \frac{{A{M_1}}}{{A{\rm{D}}}} = \frac{{IM}}{{I{\rm{D}}}} = \frac{1}{3}\end{array} \right\} \Rightarrow \frac{{A{N_1}}}{{AF}} = \frac{{A{M_1}}}{{A{\rm{D}}}}\\\left. \begin{array}{l} \Rightarrow {M_1}{N_1}\parallel DF\\DF \subset \left( {DEF} \right)\end{array} \right\} \Rightarrow {M_1}{N_1}\parallel \left( {DEF} \right)\end{array}\)
c) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}N{N_1}\parallel AB\parallel EF\\EF \subset \left( {DEF} \right)\end{array} \right\} \Rightarrow N{N_1}\parallel \left( {DEF} \right)\\{M_1}{N_1}\parallel \left( {DEF} \right)\\{M_1}{N_1},N{N_1} \subset \left( {MN{N_1}{M_1}} \right)\end{array} \right\} \Rightarrow \left( {MN{N_1}{M_1}} \right)\parallel \left( {DEF} \right)\)
a) \(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AD\parallel BC\)
Mà \(A{\rm{D}} \subset \left( {ADF} \right)\)
\( \Rightarrow BC\parallel \left( {A{\rm{D}}F} \right)\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AF\parallel BE\)
Mà \(A{\rm{F}} \subset \left( {ADF} \right)\)
\( \Rightarrow BE\parallel \left( {A{\rm{D}}F} \right)\)
Ta có:
\(\left. \begin{array}{l}BC\parallel \left( {A{\rm{D}}F} \right)\\BE\parallel \left( {A{\rm{D}}F} \right)\\BC,BE \subset \left( {CBE} \right)\end{array} \right\} \Rightarrow \left( {CBE} \right)\parallel \left( {A{\rm{D}}F} \right)\)
b) Do \(ABCD\) và \(ABEF\) là hai hình vuông có chung cạnh \(AB\) nên các đường chéo \(AC,BF\) bằng nhau.
Theo đề bài ta có: \(AM = BN\)
\( \Rightarrow \)\(\frac{{AM}}{{AC}} = \frac{{BN}}{{BF}}\)
Ta có:
\(MM'\parallel C{\rm{D}} \Rightarrow \frac{{AM}}{{AC}} = \frac{{AM'}}{{A{\rm{D}}}}\)
\(NN'\parallel AB \Rightarrow \frac{{BN}}{{BF}} = \frac{{AN'}}{{AF}}\)
\(\left. \begin{array}{l} \Rightarrow \frac{{AM'}}{{A{\rm{D}}}} = \frac{{AN'}}{{AF}} \Rightarrow M'N'\parallel DF\\M'N' \subset \left( {MNN'M'} \right)\end{array} \right\} \Rightarrow DF\parallel \left( {MNN'M'} \right)\)
\(\left. \begin{array}{l}NN'\parallel EF\\{\rm{NN}}' \subset \left( {MNN'M'} \right)\end{array} \right\} \Rightarrow EF\parallel \left( {MNN'M'} \right)\)
\(\left. \begin{array}{l}DF\parallel \left( {MNN'M'} \right)\\EF\parallel \left( {MNN'M'} \right)\\C{\rm{D}},DF \subset \left( {DEF} \right)\end{array} \right\} \Rightarrow \left( {DEF} \right)\parallel \left( {MNN'M'} \right)\)
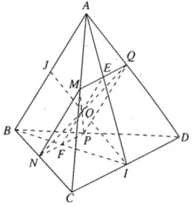
a)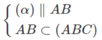 
⇒ (α) ∩ (ABC) = MN và MN // AB
Ta có N ∈ (BCD) và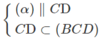 
Nên ⇒ (α) ∩ (BCD) = NP và NP // CD
Ta có P ∈ (ABD)
Và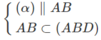 
nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
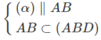nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
Do đó MN // PQ và NP // MQ, Vậy tứ giác MNPQ là hình bình hành.
b) Ta có: MP ∩ NQ = O. Gọi I là trung điểm của CD.
Trong tam giác ACD có : MQ // CD ⇒ AI cắt MQ tại trung điểm E của MQ.
Trong tam giác ACD có : NP // CD ⇒ BI cắt NP tại trung điểm F của NP.
Vì MNPQ là hình bình hành nên ta có
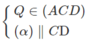
EF // MN ⇒ EF // AB
Trong ΔABI ta có EF // AB suy ra : IO cắt AB tại trung điểm J
⇒ I, O, J thẳng hàng
⇒ O ∈ IJ cố định.
Vì M di động trên đoạn AC nên Ochạy trong đoạn IJ .
Vậy tập hợp các điểm O là đoạn IJ.
Theo mình thì là C