Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

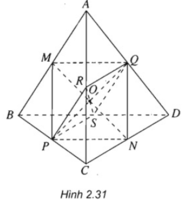
Trong tam giác ABC ta có:
MP // AC và MP = AC/2.
Trong tam giác ACD ta có:
QN // AC và QN = AC/2.
Từ đó suy ra {MP // QN}
⇒ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: PR // QS và PR = QS = AB/2. Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.

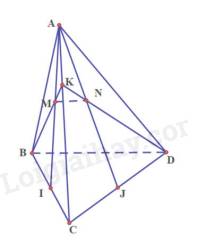
Giả sử K là trung điểm của AC
Suy ra M,N lần lượt là trọng tâm của tam giác ABC và tam giác ACD
Do đó, tam giác KBC có:\(\frac{{KM}}{{KB}} = \frac{{KN}}{{KD}} = \frac{1}{3}\)
Suy ra MN // BD
Chứng minh tương tự với trường hợp K bất kỳ

a) Ta có: MP cắt BC tại E mà BC thuộc (BCD)
Nên: E là giao điểm của đường thẳng MP với mặt phẳng (BCD).
b) Ta có: EN cắt CD tại Q mà EN thuộc (MNP)
Nên: Q là giao điểm của đường thẳng CD với mặt phẳng (MNP).
c) Ta có: P thuộc (MNP) và (ACD)
Q thuộc (MNP) và (ACD)
Nên PQ là giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).
d) △ACN có: \(\dfrac{AP}{AC}=\dfrac{AG}{AN}=\dfrac{2}{3}\)
Suy ra: PG // CN
Do đó: △PIG đồng dạng với △NIC
Do đó: C, I, G thẳng hàng.


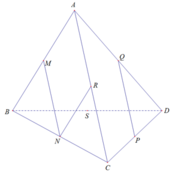
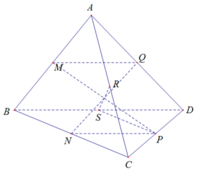

Đề bài nếu đúng thế này thì đề sai, Q là trung điểm AC, R là trung điểm BD, S là trung điểm MN thì R,Q,S thẳng hàng nên không thể tạo thành mặt phẳng (RQS)