Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

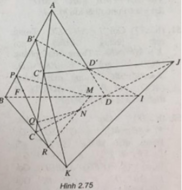
a) Chú ý rằng I, J, K thẳng hàng vì chúng cùng thuộc giao tuyến của hai mặt phẳng (CBD) và (C'B'D')
b) 4. Vì 4 điểm không đồng phẳng sẽ tạo nên 1 tứ diện => có 4 mặt

Đáp án A
A, B, C không thẳng hàng
⇒ Giao điểm của AB, AC, BC với (P) nằm trên giao tuyến của (ABC) và (P)

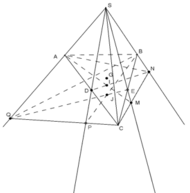
a) Ta thấy:
+ G là trọng tâm tam giác ABC ⇒ G ∈ BD ⇒ G ∈ BD
+ I ∈ DN (theo cách dựng hình).
+ J ∈ BP (theo cách dựng hình).
⇒ S, I, J, G ∈ mp(SPN)
Tương tự ⇒ S, I, J, G ∈ mp(SQM)
Vậy S, I, J, G là điểm chung của mp(SPN) và mp(SQM)
b)
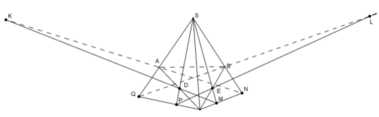
Ta thấy:
+ S = PD ∩ EM
+ K ∈ DM
+ L ∈ PE
⇒ S, K, L ∈ (SPM)
Tương tự ⇒ S, K, L ∈ (SQN)
Vậy S, K, L là điểm chung của (SPM) và (SQN)

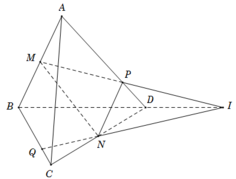
Ta có giao tuyến của 2 mp (ABD) và (BCD) là BD.
Lại có I ∈ M P ⊂ A B D I ∈ N Q ⊂ B C D ⇒ I thuộc giao tuyến của (ABD) và (BCD).
=> I thuộc BD => 3 điểm I; B; D thẳng hàng.
Chọn B.

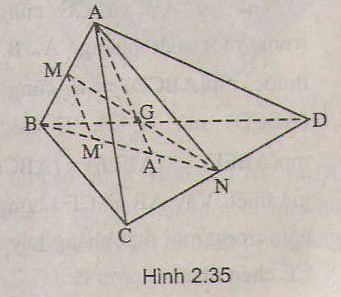
NH cắt MG \(\Rightarrow N;H;M;G\) đồng phẳng
Ba mặt phẳng \(\left(ABC\right);\left(BCD\right);\left(MGNH\right)\) cắt nhau theo 3 giao tuyến phân biệt là \(MG;NH;BC\Rightarrow\) 3 giao tuyến này song song hoặc đồng quy
Mà \(MG\) cắt NH tại I \(\Rightarrow MG;NH;BC\) đồng quy tại I
\(\Rightarrow B;C;I\) thẳng hàng
P/s: các em cấp 2 bây giờ đáng sợ thật, bay vô trả lời câu hỏi cấp 3 như 1 vị thần mặc dù có khi chẳng hiểu câu hỏi đề cập đến điều gì cả :(
Khẳng định A) A,C,I thẳng hàng