Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Vì I, J lần lượt là trung điểm của BD, CD nên IJ là đường trung bình của tam giác BCD. Từ đó suy ra: IJ // BC (3) .
- Từ (1) và (3) suy ra: MN // IJ .
→ Vậy tứ giác MNJI là hình thang.
+) Để MNJI là hình bình hành thì: MI// NJ.
- Lại có ba mặt phẳng (MNJI); (ABD); (ACD) đôi một cắt nhau theo các giao tuyến là MI, NJ, AD nên theo định lý 1 ta có: MI // AD // NJ (4)
- Mà I; J lần lượt là trung điểm BD,CD (5)
- Từ (4)và (5) suy ra: M, N lần lượt là trung điểm của AB, AC.
⇒ Vậy điều kiện để hình thang MNJI trở thành hình bình hành là M, N lần lượt là trung điểm của AB, AC.

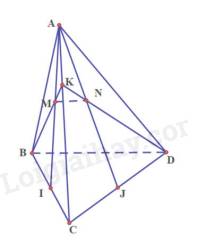
Giả sử K là trung điểm của AC
Suy ra M,N lần lượt là trọng tâm của tam giác ABC và tam giác ACD
Do đó, tam giác KBC có:\(\frac{{KM}}{{KB}} = \frac{{KN}}{{KD}} = \frac{1}{3}\)
Suy ra MN // BD
Chứng minh tương tự với trường hợp K bất kỳ

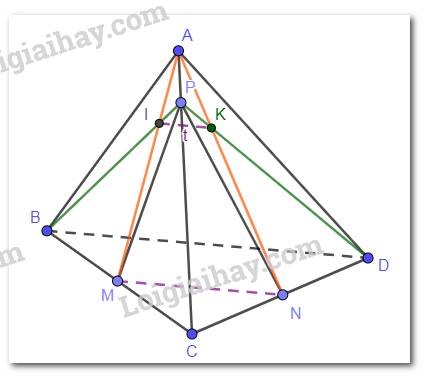
a) Gọi giao điểm của AM và BP là I, giao điểm của AN và DP là K.
Ta có IK đều thuộc mặt phẳng (AMN) và (BPD) suy ra IK là giao tuyến của hai mặt phẳng này.
Như vậy, d là đường thẳng đi qua I và K.
b) Ta có: \(mp\left( {AMN} \right) \cap mp\left( {BPD} \right) = IK\).
\(mp\left( {AMN} \right) \cap mp\left( {BCD} \right) = MN\) \(\;\).
\(mp\left( {BPD} \right) \cap mp\left( {BCD} \right) = BD\).
Mà MN // BD (do MN là đường trung bình của tam giác BCD) suy ra IK // BD.
Như vây, d song song với BD.

a) △ABC có M và N là trung điểm của AB, BC nên MN // AC (1)
△ACD có P và Q là trung điểm của CD, DA nên PQ // AC (2)
△SMN có I và J là trung điểm của SM, SN nên IJ // MN (3)
△SPQ có L và K là trung điểm của SQ, SP nên LK // PQ (4)
Từ (1)(2)(3)(4) suy ra IJ // LK. Do đó: I, J, K, L đồng phẳng.
Ta có: \(\dfrac{MN}{AC}=\dfrac{QP}{AC}=\dfrac{1}{2}\)
\(\dfrac{IJ}{MN}=\dfrac{LK}{PQ}=\dfrac{1}{2}\)
Từ (6)(7) suy ra: IJ = LK mà IJ // LK
Do đó: IJKL là hình bình hành.
b) Ta có: M, P lần lượt là trung điểm của AB, CD
Suy ra: MP // BC (1)
△SMP có: I, K là trung điểm của SM, SP
Suy ra: IK // MP (2)
Từ (1)(2) suy ra: IK // BC.
c) Ta có: J là điểm chung của hai mặt phẳng (IJKL) và (SBC)
Mà: IK // BC
Từ J kẻ Jx sao cho Jx // BC. Do đó, Jx là giao tuyến của hai mặt phẳng (IJKL) và (SBC).

Ta có N là trung điểm của BC
Suy ra A B → + A C → = 2 A N →
Lại có: A D → = 2 A Q → (Q là trung điểm của AD)
Do đó A B → + A C → + A D → = 2 A N → + 2 A Q → = 2 A N → + A Q → (1)
Tạ lại có G là trọng tâm của tứ diện ABCD nên G là trung điểm của NQ (tính chất trọng tâm của tứ diện) ⇒ A N → + A Q → = 2 A G → (2)
Từ (1) và (2) suy ra A B → + A C → + A D → = 4 A G → .
Đáp án A

Tham khảo:
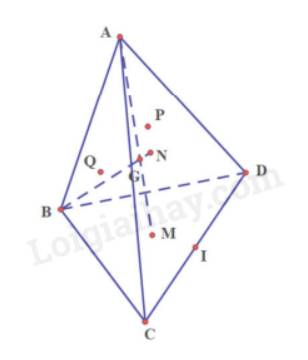
a) Ta có: M là trọng tâm của tam giác BCD
Nên M nằm trên trung tuyến BI (1)
Ta có: N là trọng tâm của tam giác ACD
Nên N nằm trên trung tuyến AI (2)
Từ (1) và (2) suy ra M và N thuộc mp (ABI)
b) Gọi H, K lần lượt là trung điểm của AG, BG
Ta có: HK // AB
AB // MN
Suy ra MN // HK
Theo định lý Ta-let, ta có: \(\frac{{GM}}{{GH}} = \frac{{GN}}{{GK}} = \frac{{MN}}{{HK}}(1)\)
Ta có:\(\frac{{HK}}{{AB}} = \frac{1}{2},\frac{{MN}}{{AB}} = \frac{1}{3}\)
Do đó \(\frac{{MN}}{{AB}}:\frac{{HK}}{{AB}} = \frac{2}{3} \Rightarrow \frac{{MN}}{{HK}} = \frac{2}{3}(2)\)
Từ (1) và (2) suy ra\(\frac{{GM}}{{GH}} = \frac{2}{3}GH = \frac{1}{2}GA \Rightarrow \frac{{GM}}{{\frac{1}{2}GA}} = \frac{2}{3} \Rightarrow \frac{{GM}}{{GA}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GN}}{{GB}} = \frac{1}{3}\)
c) Gọi H, K lần lượt là trung điểm của BC, BD
Tam giác AHD có:\(\frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Suy ra: QM // AD
Do đó, tam giác QGM đồng dạng với tam giác DGA
Nên D, G, Q thẳng hàng
Ta có: QM // AD nên \(\frac{{QM}}{{AD}} = \frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Mà \(\frac{{QM}}{{AD}} = \frac{{QG}}{{GD}}\)
Do đó:\(\frac{{QG}}{{GD}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GP}}{{GC}} = \frac{1}{3}\)
Suy ra điều cần chứng minh.

a: Gọi E là trung điểm của AB
ΔABC đều nên CE vuông góc AB
ΔABD đều nên DE vuông góc AB
=>AB vuông góc (CDE)
=>AB vuông góc CD
b: Xét ΔCAB có CN/CB=CM/CA
nên MN//AB và MN=1/2AB
Xét ΔDAB có DQ/DA=DP/DB
nên PQ//AB và PQ/AB=DQ/DA=1/2
=>MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Xét ΔADC có AQ/AD=AM/AC
nên QM//DC
=>QM vuông góc AB
=>QM vuông góc QP
=>MNPQ là hình chữ nhật
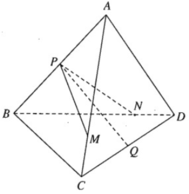
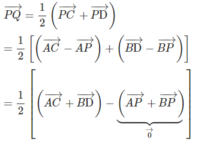
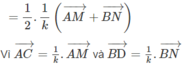
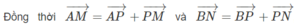
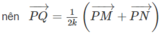
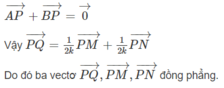
Ta có:
suy ra MN // BC (1) (Định lý Ta-lét đảo).
- Lại có: MN ∩ (MNI) (2)
- Từ (1) và (2) suy ra: BC // (MNI)