

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




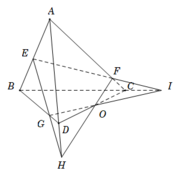
Trong mặt phẳng (ACD) : FN cắt CD tại H ⇒ H ∈ (EFG) và H ∈ (BCD) ⇒ H ∈ MG là giao tuyến của (EFG) và (BCD) hay FN, MG, CD đồng quy tại H ⇒ M, N, F, G đồng phẳng
Đáp án D

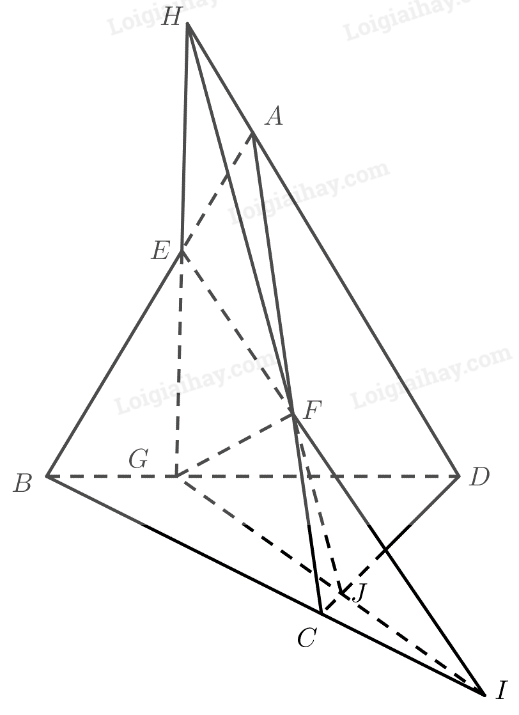
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}G \in \left( {EFG} \right)\\G \in BD \subset \left( {BCD} \right)\end{array} \right\} \Rightarrow G \in \left( {EFG} \right) \cap \left( {BCD} \right)\\\left. \begin{array}{l}I \in EF \subset \left( {EFG} \right)\\I \in BC \subset \left( {BCD} \right)\end{array} \right\} \Rightarrow I \in \left( {EFG} \right) \cap \left( {BCD} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {EFG} \right)\) và \(\left( {BCD} \right)\) là đường thẳng \(GI\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}F \in \left( {EFG} \right)\\F \in AC \subset \left( {ACD} \right)\end{array} \right\} \Rightarrow F \in \left( {EFG} \right) \cap \left( {ACD} \right)\\\left. \begin{array}{l}H \in EG \subset \left( {EFG} \right)\\H \in A{\rm{D}} \subset \left( {ACD} \right)\end{array} \right\} \Rightarrow H \in \left( {EFG} \right) \cap \left( {ACD} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {EFG} \right)\) và \(\left( {ACD} \right)\) là đường thẳng \(HF\).
b) Gọi \(J\) là giao điểm của \(CD\) và \(IG\).
Ta có:
\(\left. \begin{array}{l}J \in IG \subset \left( {EFG} \right)\\J \in C{\rm{D}} \subset \left( {ACD} \right)\end{array} \right\} \Rightarrow J \in \left( {EFG} \right) \cap \left( {ACD} \right)\)
Mà \(F \in \left( {EFG} \right) \cap \left( {ACD} \right),H \in \left( {EFG} \right) \cap \left( {ACD} \right)\) (theo chứng minh phần a).
Do đó ba điểm \(H,F,J\) thẳng hàng.
Vậy ba đường thẳng \(CD,IG,HF\) cùng đi điểm \(J\).

a: Xét ΔAMB có ME là đường phân giác
nên AE/EB=AM/MB=AM/MC(4)
XétΔAMC có MD là đường phân giác
nên AD/DC=AM/MC(5)
Từ (4) và (5) suy ra AE/EB=AD/DC
b: Xét ΔABC có
AE/EB=AD/DC
nên ED//BC
Xét ΔABM có EI//BM
nên EI/BM=AE/AB(1)
Xét ΔACM có ID//MC
nên ID/MC=AD/AC(2)
Xét ΔABC có
ED//BC
nên AE/AB=AD/AC(3)
Từ (1), (2) và (3) suy ra EI/BM=DI/MC
mà BM=CM
nên EI=DI
hay I là trung điểm của ED

a. Do \(\left\{{}\begin{matrix}AB\perp BC\\AB\perp BD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(BCD\right)\Rightarrow AB\perp CD\) (1)
Mặt khác BCD vuông tại C \(\Rightarrow CD\perp BC\) (2)
(1);(2) \(\Rightarrow CD\perp\left(ABC\right)\Rightarrow CD\perp AC\Rightarrow\Delta ACD\) vuông tại C
b. Gọi M là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}EM=\frac{1}{2}CD=a\\FM=\frac{1}{2}AB=a\end{matrix}\right.\) theo t/c đường trung bình
Mặt khác \(\left\{{}\begin{matrix}AB//FM\\CD//EM\end{matrix}\right.\) \(\Rightarrow\left(AB;CD\right)=\left(FM;EM\right)=\widehat{FEM}\)
Áp dụng định lý hàm cos cho tam giác \(FME\)
\(cos\widehat{FEM}=\frac{MF^2+EF^2-ME^2}{2ME.EF}=\frac{\sqrt{3}}{2}\Rightarrow\widehat{FEM}=30^0\)