Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
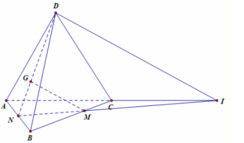
Gọi N là trung điểm của AB.Trong mặt phẳng (ABC)
gọi I là giao điểm của MN và AC.Ta có N G N D = N M N I = 1 3 ⇒ G M / / D I
Mà D I ⊂ A C D ⇒ G M / / A C D .

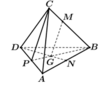
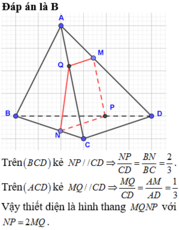
Gọi P là trung điểm của AD.
Vì G là trọng tâm tam giác BCD nên 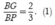
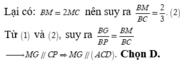

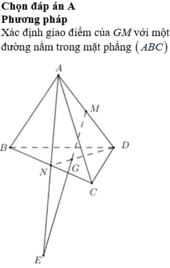
Đáp án C
Do 4 điểm A, M, G, N cùng thuộc mặt phẳng (AND) khi đó MG cắt AN suy ra giao điểm của đường thẳng MG và mặt phẳng (ABC) là giao điểm của đường thẳng MG và đường thẳng AN
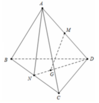

Đáp án A
Giả sử tứ diện ABCD có AB;AC'AD đội một vuông góc ⇒ V A B C D = A B . A C . A D 6
Khi đó tứ diện MNPQ có MN;MP;MQ đội một vuông góc ⇒ V M . N P Q = M N . M P . M Q 6
Ta chứng minh được M N A B + M P A C + M Q A D = 1 ( dựa vào định lý Thalet), khi đó
M N . M P . M Q = A B . A C . A D . M N A B . M P A C . M Q A D ≤ A B . A C . A D . M N A B + M P A C + M Q A D 3 27 = A B . A C . A D 27
Vậy V M . N P Q = M N . M P . M Q 6 ≤ 1 27 . A B . A C . A D 6 = V 27 → V max = V 27
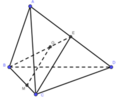

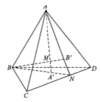

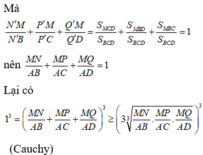

Đáp án A