Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

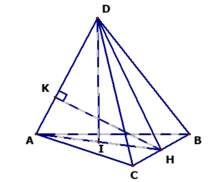
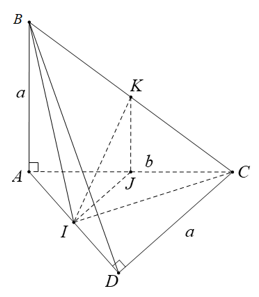
CMR: DI ⊥ (ABC).
● AD = a, DH = a ΔDAH cân tại D.
- Mặt khác I là trung điểm của AH nên DI ⊥ AH.
● BC ⊥ (ADH) ⇒ BC ⊥ DI.
⇒ DI ⊥ (ABC).

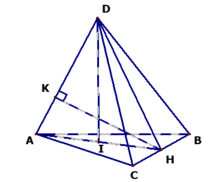
Tính khoảng cách giữa AD và BC.
● Trong ΔADH vẽ đường cao HK tức là HK ⊥ AD (1)
- Mặt khác BC ⊥ (ADH) nên BC ⊥ HK (2)
- Từ (1) và (2) ta suy ra d(AD, BC) = HK.
● Xét ΔDIA vuông tại I ta có:
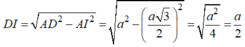
● Xét ΔDAH ta có:
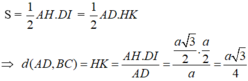

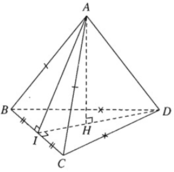
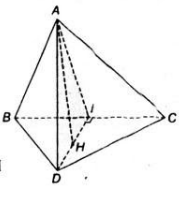
a) Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên AI ⊥ BC. Tương tự tam giác DBC cân đỉnh D và có có I là trung điểm của BC nên DI ⊥ BC. Ta suy ra:
BC ⊥ (AID) nên BC ⊥ AD.
b) Vì BC ⊥ (AID) nên BC ⊥ AH
Mặt khác AH ⊥ ID nên ta suy ra AH vuông góc với mặt phẳng (BCD).

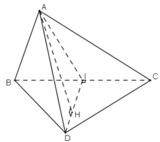
a) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao:
AI ⊥ BC
+) Tương tự, tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao:
DI ⊥ BC
+) Ta có: 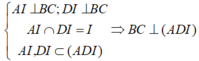
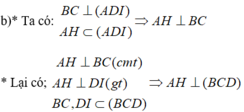

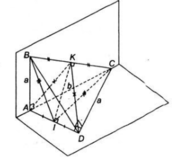


Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.

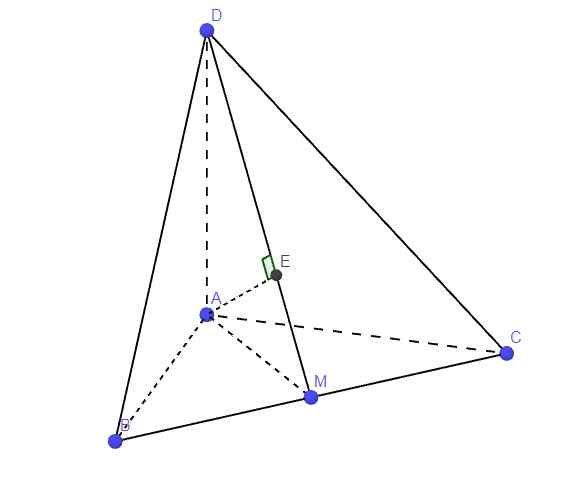
a.
Do \(AB=AC\Rightarrow\Delta ABC\) cân tại A
\(\Rightarrow AM\) là trung tuyến đồng thời là đường cao
\(\Rightarrow AM\perp BC\) (1)
Mà \(\left\{{}\begin{matrix}AD\perp AB\left(gt\right)\\AD\perp AC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(ABC\right)\Rightarrow AD\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(ADM\right)\)
b.
Từ A kẻ \(AE\perp DM\) (E thuộc DM)
Do \(BC\perp\left(ADM\right)\Rightarrow BC\perp AE\)
\(\Rightarrow AE\perp\left(BCD\right)\Rightarrow AE=d\left(A;\left(BCD\right)\right)\)
\(BC=\sqrt{AB^2+AC^2}=5\sqrt{2}\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5\sqrt{2}}{2}\)
Hệ thức lượng trong tam giác vuông ADM:
\(AE=\dfrac{AD.AM}{\sqrt{AD^2+AM^2}}=\dfrac{5\sqrt{3}}{3}\)
c.
Do \(AD\perp\left(ABC\right)\) theo cmt \(\Rightarrow AM\) là hình chiếu vuông góc của DM lên (ABC)
\(\Rightarrow\widehat{DMA}\) là góc giữa DM và (ABC)
\(tan\widehat{DMA}=\dfrac{AD}{AM}=\sqrt{2}\Rightarrow\widehat{DMA}\approx54^044'\)




CMR: BC ⊥ (ADH) và DH = a.
● Δ ABC đều, H là trung điểm BC nên AH BC, AD BC
⇒ BC ⊥ (ADH) ⇒ BC ⊥ DH.
⇒ DH = d(D, BC) = a