Cho tứ diện ABCD có I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chứng minh rằng IJ // CD ?

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

SG

Sách Giáo Khoa

21 tháng 5 2017

Cho tứ diện ABCD có I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chứng minh rằng IJ // CD ?

#Toán lớp 11

1

NT

Nguyen Thuy Hoa

25 tháng 5 2017

Đường thẳng và mặt phẳng trong không gian, Quan hệ song song

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PT

Pham Trong Bach

24 tháng 3 2019

Cho tứ diện ABCD có I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chứng minh rằng: IJ // CD.

#Toán lớp 11

1

CM

Cao Minh Tâm

24 tháng 3 2019

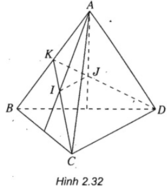
Giải sách bài tập Toán 11 | Giải sbt Toán 11

Gọi K là trung điểm của AB.

Vì I là trọng tâm của tam giác ABC nên I ∈ KC và vì J là trọng tâm của tam giác ABD nên J ∈ KD.

Từ đó suy ra

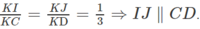
Giải sách bài tập Toán 11 | Giải sbt Toán 11

2T

24.Trần Thị Quỳnh Như

12 tháng 12 2021

Cho tứ diện ABCD Gọi I,J lần lượt là trọng tâm tam giác ABC,ABD và E,F lần lượt là trung điểm của BC,AC

a/Chứng minh IJ//(ACD)

b/Tìm giao tuyến của và ABD Giúp mk vs mk cần gấp ạ mk cảm ơn

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

12 tháng 12 2021

Câu b đề bài thiếu, tìm giao tuyến của mặt nào và (ABD) vậy em?

TD

Thầy Đức Anh

Giáo viên VIP

21 tháng 12 2021 - olm

Cho hình chóp ABCD. I, J lần lượt là trọng tâm tam giác ADC và tam giác BCD. Chứng minh IJ // (ABD).

#Toán lớp 11

173

PP

Phạm Phương Chi

24 tháng 12 2021

TH

Tạ Hồng Nhung

25 tháng 12 2021

IJ (CIJ).

"Mở rộng" mặt phẳng (CIJ) thành (CMN).

Trong tam giác CMN:

(Do I, J lần lượt là trọng tâm tam giác ADC và tam giác BCD. )

IJ//MN (Định lý Ta-lét).

Mà MN (ABD).

Vậy IJ//(ABD).

PT

Pham Trong Bach

20 tháng 4 2019

Cho tứ diện ABCD. Gọi G 1 và G 2 lần lượt là trọng tâm của tam giác ACD và BCD. Chứng minh rằng G 1 G 2 song song với các mặt phẳng (ABC) và (ABD).

#Toán lớp 11

1

CM

Cao Minh Tâm

20 tháng 4 2019

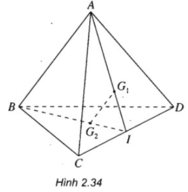
Giải sách bài tập Toán 11 | Giải sbt Toán 11

Gọi I là trung điểm của CD.

Vì G 1 là trọng tâm của tam giác ACD nên G 1 ∈ A I

Vì G 2 là trọng tâm của tam giác BCD nên G 2 ∈ B I

Ta có :

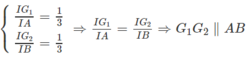
Giải sách bài tập Toán 11 | Giải sbt Toán 11

A B ⊂ ( A B C ) ⇒ G 1 G 2 / / ( A B C )

Và A B ⊂ ( A B D ) ⇒ G 1 G 2 / / ( A B D )

PT

Pham Trong Bach

11 tháng 5 2018

Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm các tam giác ABC và ABD. Trong các mệnh đề sau, mệnh đề nào đúng?

A. IJ//AB

B. IJ // DC

C. IJ//BD

D. IJ//AC

#Toán lớp 11

1

CM

Cao Minh Tâm

11 tháng 5 2018

PT

Pham Trong Bach

6 tháng 4 2017

Cho tứ diện ABCD. Gọi G 1 , G 2 , G 3 lần lượt là trọng tâm các tam giác ABC, ACD, ABD. Chứng minh rằng ( G 1 G 2 G 3 ) / / ( B C D ) .

#Toán lớp 11

1

CM

Cao Minh Tâm

6 tháng 4 2017

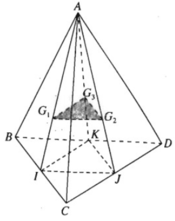
Giải sách bài tập Toán 11 | Giải sbt Toán 11

Gọi I, J và K lần lượt là trung điểm của các cạnh BC, CD và BD. Theo tính chất trọng tâm của tam giác ta có:

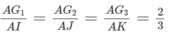
Giải sách bài tập Toán 11 | Giải sbt Toán 11

B

Buddy

14 tháng 7 2023

Cho tứ diện ABCD. Gọi G1,G2 lần lượt là trọng tâm của các tam giácABC và ABD. Chứng minh rằng đường thẳng G1G2song song với đường thẳng CD.

#Toán lớp 11

1

QT

Quoc Tran Anh Le

Giáo viên

22 tháng 9 2023

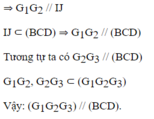
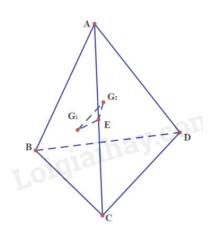
Gọi E là trung điểm AB

Ta có:\({G_1}\) là trọng tâm của tam giác ABC

Suy ra\(\frac{{E{G_1}}}{{EC}} = \frac{1}{3}(1)\)

Ta có:\({G_2}\) là trọng tâm của tam giác ABD

Suy ra\(\frac{{E{G_2}}}{{ED}} = \frac{1}{3}(2)\)

Từ (1) và (2) suy ra:\(\frac{{E{G_1}}}{{EC}} = \frac{{E{G_2}}}{{ED}}\)

Theo định lý Ta-let, suy ra:\({G_1}{G_2}//CD\)

PN

pham nhat

26 tháng 8 2023

Cho tứ diện ABCD gọiI J là trọng tâm tam giác ABC và ABD.E F là trung điểm của BC và AC.

a.CM IJ//CD

b.tìm giao tuyến của (DEF) và (ABD)

#Toán lớp 11

0

HN

Hàn Nhật Hạ

20 tháng 4 2022

Câu 1: Cho tứ diện ABCD có hai mặt ABC và ABD là hai tam giác đều.

a. Chứng minh rằng AB và CD vuông góc với nhau.

b. Gọi M, N, P, P, Q lần lượt là trung điểm của các cạnh AC, BC, BD, DA. Chứng minh rằng tứ giác MNPQ là hình chữ nhật

giúp mk vs ạ!!!

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

27 tháng 6 2023

a: Gọi E là trung điểm của AB

ΔABC đều nên CE vuông góc AB

ΔABD đều nên DE vuông góc AB

=>AB vuông góc (CDE)

=>AB vuông góc CD

b: Xét ΔCAB có CN/CB=CM/CA

nên MN//AB và MN=1/2AB

Xét ΔDAB có DQ/DA=DP/DB

nên PQ//AB và PQ/AB=DQ/DA=1/2

=>MN//PQ và MN=PQ

=>MNPQ là hình bình hành

Xét ΔADC có AQ/AD=AM/AC

nên QM//DC

=>QM vuông góc AB

=>QM vuông góc QP

=>MNPQ là hình chữ nhật