Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
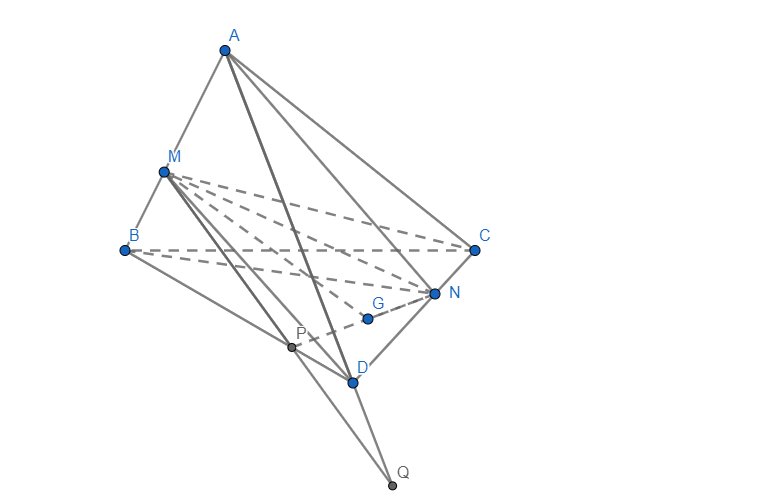
\(\left\{{}\begin{matrix}M\in\left(MCD\right)\\M\in AB\subset\left(NAB\right)\end{matrix}\right.\)\(\Rightarrow M\in\left(MCD\right)\cap\left(NAB\right)\)
\(\left\{{}\begin{matrix}N\in CD\subset\left(MCD\right)\\N\in\left(NAB\right)\end{matrix}\right.\)\(\Rightarrow N\in\left(MCD\right)\cap\left(NAB\right)\)
\(\Rightarrow MN=\left(MCD\right)\cap\left(NAB\right)\)
b) Trong mp(BCD), gọi \(P=NG\cap BD\)
Trong mp(BAD), gọi \(Q=PM\cap AD\)
Ta có:
\(\left\{{}\begin{matrix}N\in\left(GMN\right)\\N\in CD\subset\left(ACD\right)\end{matrix}\right.\)\(\Rightarrow N\in\left(GMN\right)\cap\left(ACD\right)\)
Ta có:
\(\left\{{}\begin{matrix}Q\in MP\subset\left(GMN\right)\\Q\in AD\subset\left(ACD\right)\end{matrix}\right.\)\(\Rightarrow Q\in\left(GMN\right)\cap\left(ACD\right)\)
\(\Rightarrow NQ=\left(GMN\right)\cap\left(ACD\right)\)

a) Ta có:
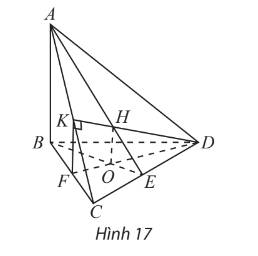
\(\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot C{\rm{D}}\\BE \bot CE\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABE} \right)\)
Lại có \(C{\rm{D}} \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {ABE} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot DF\\DF \bot BC\end{array} \right\} \Rightarrow DF \bot \left( {ABC} \right)\\\left. \begin{array}{l} \Rightarrow DF \bot AC\\DK \bot AC\end{array} \right\} \Rightarrow AC \bot \left( {DFK} \right)\end{array}\)
Lại có \(AC \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {DFK} \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left( {ADC} \right) \bot \left( {ABE} \right)\\\left( {ADC} \right) \bot \left( {DFK} \right)\\\left( {ABE} \right) \cap \left( {DFK} \right) = OH\end{array} \right\} \Rightarrow OH \bot \left( {ADC} \right)\)

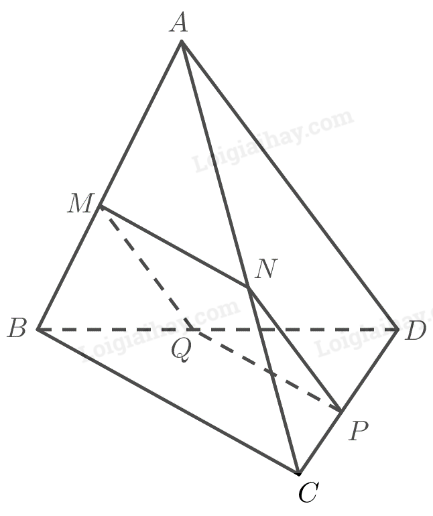
a) Ta có:
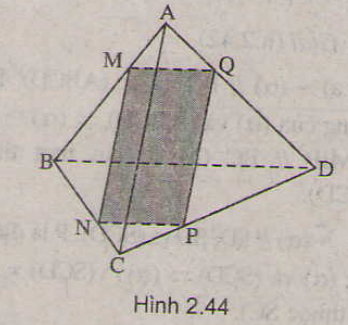
\(\begin{array}{l}MN = \left( \alpha \right) \cap \left( {ABC} \right)\\PQ = \left( \alpha \right) \cap \left( {BC{\rm{D}}} \right)\\BC = \left( {ABC} \right) \cap \left( {BC{\rm{D}}} \right)\\MN\parallel BC\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MN\parallel PQ\parallel BC\) (1).
\(\begin{array}{l}MQ = \left( \alpha \right) \cap \left( {ABD} \right)\\NP = \left( \alpha \right) \cap \left( {AC{\rm{D}}} \right)\\A{\rm{D}} = \left( {ABD} \right) \cap \left( {AC{\rm{D}}} \right)\\MQ\parallel A{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MQ\parallel NP\parallel A{\rm{D}}\) (2).
Từ (1) và (2) suy ra \(MNPQ\) là hình bình hành.
b) Để \(MNPQ\) là hình thoi thì \(MN = NP\).
Ta có:
\(\begin{array}{l}MN\parallel BC \Rightarrow \frac{{MN}}{{BC}} = \frac{{AN}}{{AC}}\\NP\parallel A{\rm{D}} \Rightarrow \frac{{NP}}{{A{\rm{D}}}} = \frac{{CN}}{{AC}} \Rightarrow \frac{{MN}}{{A{\rm{D}}}} = \frac{{CN}}{{AC}}\end{array}\)
Ta có:
\(\begin{array}{l}\frac{{AN}}{{AC}} + \frac{{CN}}{{AC}} = 1 \Leftrightarrow \frac{{MN}}{{BC}} + \frac{{MN}}{{A{\rm{D}}}} = 1 \Leftrightarrow MN.\left( {\frac{1}{{BC}} + \frac{1}{{A{\rm{D}}}}} \right) = 1\\ \Leftrightarrow MN.\frac{{BC + A{\rm{D}}}}{{BC.A{\rm{D}}}} = 1 \Leftrightarrow MN = \frac{{BC.A{\rm{D}}}}{{BC + A{\rm{D}}}}\end{array}\)
Vậy nếu \(MN = \frac{{BC.A{\rm{D}}}}{{BC + A{\rm{D}}}}\) thì \(MNPQ\) là hình thoi.