Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: TH1: Chọn 1 điểm trong 2 điểm M,N; 1 điểm trong 3 điểm P,Q,R
Số cách chọn 1 điểm trong 2 điểm M,N là 2 cách
Số cách chọn 1 điểm trong 3 điểm P,Q,R là 3 cách
=>Có 2*3=6(cách)
TH2: Vẽ đường thẳng PQR
=>Có 1 cách
TH3: Vẽ đường thẳng MN
=>Có 1 cách
Tổng số đường thẳng là:
6+1+1=8(đường)
b: TH1: Chọn 1 điểm trong 5 điểm thẳng hàng, chọn 1 điểm trong 4 điểm không thẳng hàng
Số cách chọn 1 điểm trong 5 điểm thẳng hàng là 5 cách
Số cách chọn 1 điểm trong 4 điểm không thẳng hàng là 4 cách
=>Có 5*4=20 đường thẳng
TH2: Vẽ 1 đường thẳng đi qua 5 điểm thẳng hàng
=>Có 1 đường thẳng
TH3: Chọn 2 điểm trong 4 điểm không thẳng hàng
=>Có \(C^2_4=6\left(đường\right)\)
Số đường thẳng tất cả là:
20+1+6=27(đường)

Số đường thẳng vẽ được là:
1+3*17+\(C^3_{17}=732\left(đường\right)\)

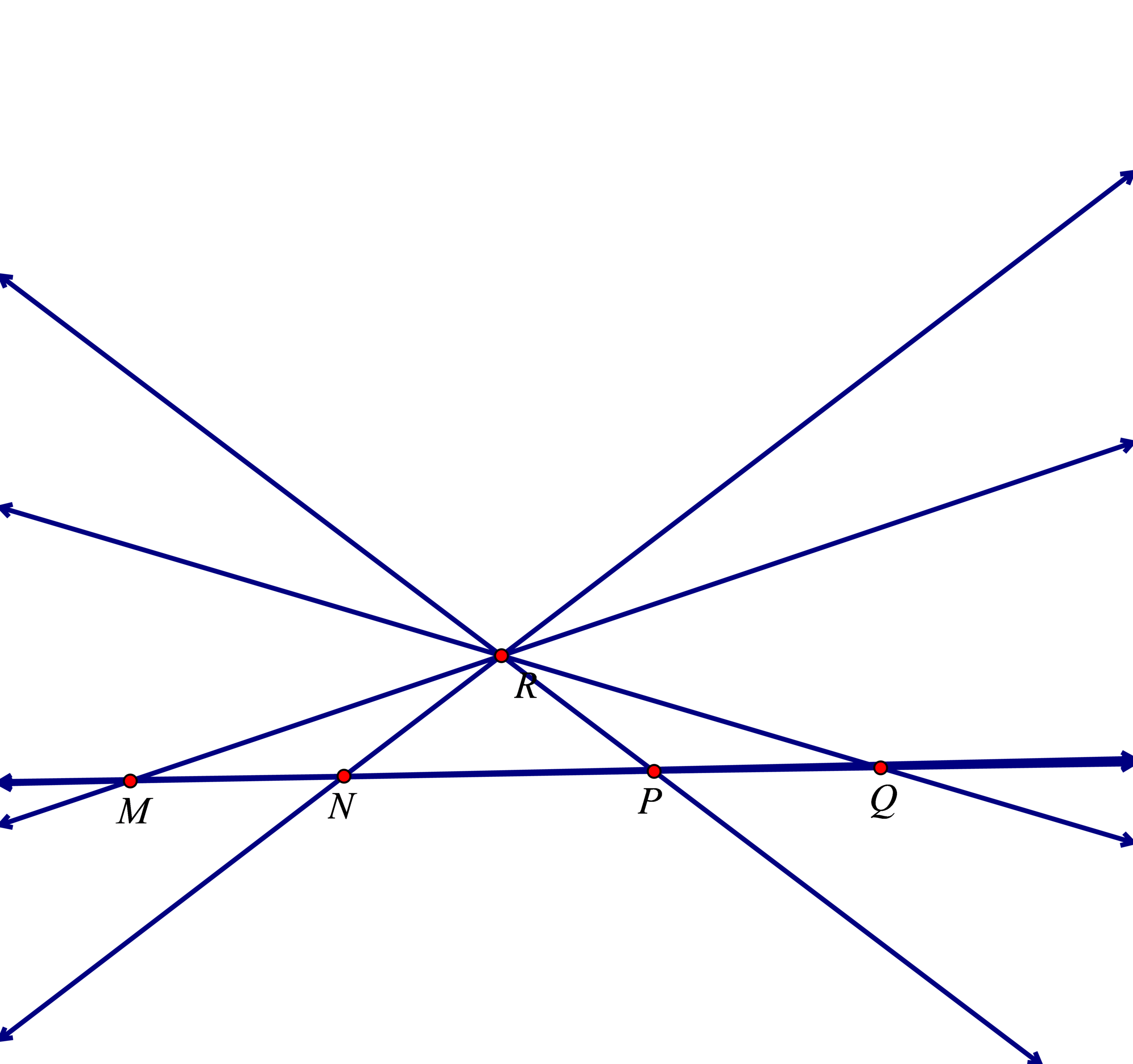
a) Có 5 đường thẳng, đó là đường thẳng MQ, RM, RN, RP, RQ.
b) Các tia gốc P là: PM, PN, PQ, PR. Hai tia PM, PN trùng nhau. Hai tia PM, PQ đối nhau.

vẽ được 2 đường thẳng
đó là đường thẳng PQR và đường thẳng MN
CÓ ĐÚNG KHÔNG BẠN THÂN YÊU!!!
M N P Q R có 9 đường thẳng đó là : MN;MP;MR;MQ;PN;PQ;QR;NQ;MR

a)Nếu trong 6 điểm đó không có ba điểm nào thẳng hàng thì sẽ vẽ được số đường thẳng là
\(\frac{6.\left(6-1\right)}{2}=\frac{6.5}{2}=15\)(đường thẳng)
b) Nếu 100 điểm trong đó không có 3 điểm nào thẳng hàng thì vẽ được số đường thẳng đi qua các cặp điểm là:
\(\frac{100.\left(100-1\right)}{2}=4950\)(đường thẳng)
