K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

4 tháng 9 2021
a: Xét tứ giác BHCD có
CH//BD
BH//CD
Do đó: BHCD là hình bình hành

TH
23 tháng 11 2021
Cho hình thoi 𝐴𝐵𝐶𝐷 (𝐴መ > 90). Gọi 𝐸 là hình chiếu vuông góc của 𝐴 trên 𝐵𝐶, 𝐹 là hình
chiếu vuông góc của 𝐶 trên 𝐴𝐷.
a) Tứ giác 𝐴𝐸𝐶𝐹 là hình gì? Vì sao?
b) 𝐵𝐷 cắt 𝐴𝐸 tại 𝐻, cắt 𝐶𝐹 tại 𝐾. Chứng minh rằng 𝐴𝐾 = 𝐶𝐻.
c) Gọi 𝐼 là giao điểm của 𝐴𝐾 và 𝐶𝐷, 𝐽 là giao điểm của 𝐶𝐻 và 𝐴𝐵. Chứng minh rằng 𝐸𝐼 ⊥ 𝐸𝐽

KV
24 tháng 4 2023
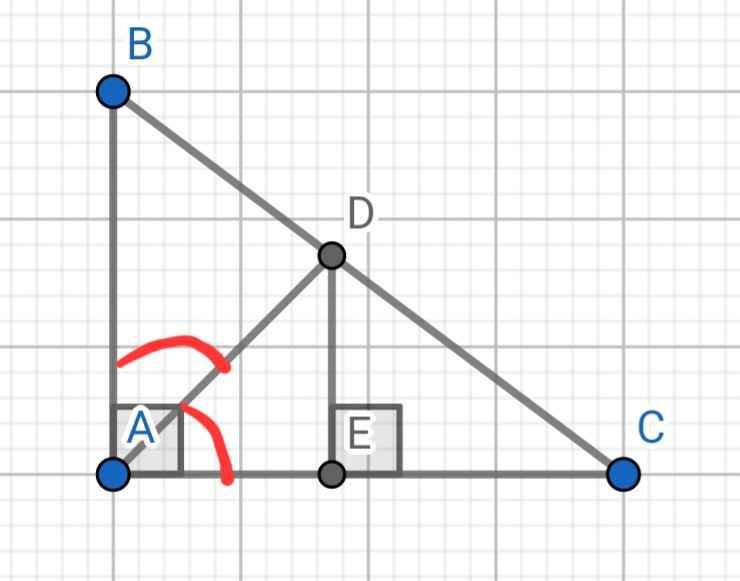
a) Do AD là đường phân giác của ∠BAC
⇒ BD/CD = AB/AC = 9/12 = 3/4
b) Xét hai tam giác vuông: ∆ABC và ∆EDC có:
∠C chung
⇒ ∆ABC ∽ ∆EDC (g-g)
24 tháng 4 2023
a: BD/CD=AB/AC=3/4
b: Xét ΔABC vuông tại A và ΔEDC vuông tại E có
góc C chung
=>ΔABC đồng dạng với ΔEDC

4 tháng 9 2021
a: Xét tứ giác BHCD có
BH//CD
CH//BD
Do đó: BHCD là hình bình hành