
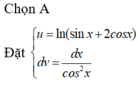



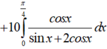







Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

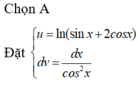











a)
Ta có \(A=\int ^{\frac{\pi}{4}}_{0}\cos 2x\cos^2xdx=\frac{1}{4}\int ^{\frac{\pi}{4}}_{0}\cos 2x(\cos 2x+1)d(2x)\)
\(\Leftrightarrow A=\frac{1}{4}\int ^{\frac{\pi}{2}}_{0}\cos x(\cos x+1)dx=\frac{1}{4}\int ^{\frac{\pi}{2}}_{0}\cos xdx+\frac{1}{8}\int ^{\frac{\pi}{2}}_{0}(\cos 2x+1)dx\)
\(\Leftrightarrow A=\frac{1}{4}\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|\sin x+\frac{1}{16}\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|\sin 2x+\frac{1}{8}\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|x=\frac{1}{4}+\frac{\pi}{16}\)
b)
\(B=\int ^{1}_{\frac{1}{2}}\frac{e^x}{e^{2x}-1}dx=\frac{1}{2}\int ^{1}_{\frac{1}{2}}\left ( \frac{1}{e^x-1}-\frac{1}{e^x+1} \right )d(e^x)\)
\(\Leftrightarrow B=\frac{1}{2}\left.\begin{matrix} 1\\ \frac{1}{2}\end{matrix}\right|\left | \frac{e^x-1}{e^x+1} \right |\approx 0.317\)
c)
Có \(C=\int ^{1}_{0}\frac{(x+2)\ln(x+1)}{(x+1)^2}d(x+1)\).
Đặt \(x+1=t\)
\(\Rightarrow C=\int ^{2}_{1}\frac{(t+1)\ln t}{t^2}dt=\int ^{2}_{1}\frac{\ln t}{t}dt+\int ^{2}_{1}\frac{\ln t}{t^2}dt\)
\(=\int ^{2}_{1}\ln td(\ln t)+\int ^{2}_{1}\frac{\ln t}{t^2}dt=\frac{\ln ^22}{2}+\int ^{2}_{1}\frac{\ln t}{t^2}dt\)
Đặt \(\left\{\begin{matrix} u=\ln t\\ dv=\frac{dt}{t^2}\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{dt}{t}\\ v=\frac{-1}{t}\end{matrix}\right.\Rightarrow \int ^{2}_{1}\frac{\ln t}{t^2}dt=\left.\begin{matrix} 2\\ 1\end{matrix}\right|-\frac{\ln t+1}{t}=\frac{1}{2}-\frac{\ln 2 }{2}\)
\(\Rightarrow C=\frac{1}{2}-\frac{\ln 2}{2}+\frac{\ln ^22}{2}\)

Lời giải:
Ta có:
\(A=\int \frac{x\sin x+\cos x}{x^2-\cos ^2x}dx=\int \frac{(\cos x-x)+x(\sin x+1)}{x^2-\cos ^2x}dx\)
\(=-\int \frac{dx}{\cos x+x}+\int \frac{x(\sin x+1)}{x^2-\cos ^2x}dx=-\int \frac{dx}{x+\cos x}+\frac{1}{2}\int (\sin x+1)\left(\frac{1}{x-\cos x}+\frac{1}{x+\cos x}\right)dx\)
\(=-\int \frac{dx}{x+\cos x}+\frac{1}{2}\int (\sin x+1)\frac{dx}{x-\cos x}+\frac{1}{2}\int (\sin x-1)\frac{dx}{x+\cos x}+\int \frac{dx}{x+\cos x}\)
\(=\frac{1}{2}\int (\sin x+1)\frac{dx}{x-\cos x}+\frac{1}{2}\int (\sin x-1)\frac{dx}{x+\cos x}\)
\(=\frac{1}{2}\int \frac{d(x-\cos x)}{x-\cos x}+\frac{1}{2}\int \frac{-d(x+\cos x)}{x+\cos x}\)
\(=\frac{1}{2}\ln |x-\cos x|-\frac{1}{2}\ln |x+\cos x|+c\)
Xét biểu thức $B$
\(B=\int \frac{\ln x-1}{x^2-\ln ^2x}dx=\int \frac{(\ln x-x)+(x-1)}{x^2-\ln ^2x}dx\)
\(=-\int \frac{dx}{x+\ln x}+\int \frac{x-1}{x^2-\ln ^2x}dx=-\int \frac{dx}{x+\ln x}+\frac{1}{2}\int \frac{(x-1)}{x}\left(\frac{1}{x-\ln x}+\frac{1}{x+\ln x}\right)dx\)
\(=-\int \frac{dx}{x+\ln x}+\frac{1}{2}\int \frac{1}{x-\ln x}.\frac{x-1}{x}dx+\frac{1}{2}\int \frac{1}{x+\ln x}.\frac{x-1}{x}dx\)
\(=-\int \frac{dx}{x+\ln x}+\frac{1}{2}\int \frac{1}{x-\ln x}.\frac{x-1}{x}dx-\frac{1}{2}\int \frac{1}{x+\ln x}.\frac{1+x}{x}dx+\int \frac{dx}{x+\ln x}\)
\(=\frac{1}{2}\int \frac{1}{x-\ln x}.\frac{x-1}{x}dx-\frac{1}{2}\int \frac{1}{x+\ln x}.\frac{1+x}{x}dx\)
\(=\frac{1}{2}\int \frac{d(x-\ln x)}{x-\ln x}-\frac{1}{2}\int \frac{d(x+\ln x)}{x+\ln x}\)
\(=\frac{1}{2}\ln |x-\ln x|-\frac{1}{2}\ln |x+\ln x|+c\)

Câu 1: Là \(ln^2x+lnx\) hay \(lnx^2+lnx\) bạn, hai cái này khác nhau lắm, viết thế kia chẳng hiểu gì cả. Biểu thức logarit nếu viết mũ, thì hoặc là viết thế này \(ln^2x\) hoặc là \(\left(lnx\right)^2\), nếu viết \(ln\left(x\right)^2\) người ta sẽ mặc định hiểu là \(ln\left(x^2\right)\)
Chắc là cái đầu, vậy ta biến đổi được:
\(lnx\left(lnx+1\right)=lnx\left(lnx+lne\right)=lnx.ln\left(x.e\right)=ln\left(x.e\right)^{lnx}\)
Câu 2: đạo hàm 4 cái ra, dễ dàng nhận ra ở đáp án d, với \(x\ge0\Rightarrow f'\left(x\right)=3x^2+4x+\frac{1}{2\sqrt{x}}>0\) luôn đồng biến nên hàm không có cực trị
Câu 3:
Phương trình hoành độ giao điểm:
\(\frac{m-x}{x+1}=2x+m\Leftrightarrow m-x=2x^2+\left(m+2\right)x+m\)
\(\Leftrightarrow2x^2+\left(m+3\right)x=0\)
Phương trình luôn có nghiệm \(x=0\) hay ít nhất 1 trong 2 điểm A; B sẽ trùng gốc tọa độ tức \(OA=0\) hoặc \(OB=0\)
Do đó ko tồn tại m thỏa mãn
Câu 4:
\(\left\{{}\begin{matrix}lnx=X\\lny=Y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2X^2+3Y^2=5\\X+4Y=3\end{matrix}\right.\)
\(\Rightarrow2\left(3-4Y\right)^2+3Y^2=5\)
\(\Leftrightarrow35Y^2-48Y+13=0\Rightarrow\left[{}\begin{matrix}Y=1\Rightarrow X=-1\\Y=\frac{13}{35}\Rightarrow X=\frac{53}{35}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}lnx=-1\\lny=1\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(e^{-1};e\right)\) \(\Rightarrow\left\{{}\begin{matrix}c=-1\\d=1\end{matrix}\right.\)
Hoặc \(\left\{{}\begin{matrix}lnx=\frac{53}{35}\\lny=\frac{13}{35}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=e^{\frac{53}{35}}=e\sqrt[35]{e^{18}}\\y=e^{\frac{13}{35}}=\sqrt[35]{e^{13}}\end{matrix}\right.\) \(\Rightarrow a=b=35\)
Đáp án b sai

a/ Tích phân này làm sao giải được nhỉ?
b/ Đặt \(\sqrt{x}=t\Rightarrow x=t^2\Rightarrow dx=2t.dt\)
\(I=\int\frac{2t^2.dt}{4-t^4}=\int\left(\frac{1}{2-t^2}-\frac{1}{2+t^2}\right)dt=\frac{1}{2\sqrt{2}}ln\left|\frac{\sqrt{2}+t}{\sqrt{2}-t}\right|+\frac{1}{\sqrt{2}}arctan\frac{\sqrt{2}}{t}+C\)
\(=\frac{1}{2\sqrt{2}}ln\left|\frac{\sqrt{2}+\sqrt{x}}{\sqrt{2}-\sqrt{x}}\right|+\frac{1}{\sqrt{2}}arctan\frac{\sqrt{2}}{\sqrt{x}}+C\)
c/ \(I=\int\frac{\sqrt{1+x^2}}{x^2}.xdx\)
Đặt \(\sqrt{1+x^2}=t\Rightarrow x^2=t^2-1\Rightarrow xdx=tdt\)
\(\Rightarrow I=\int\frac{t^2dt}{t^2-1}=\int\left(1+\frac{1}{t^2-1}\right)dt=t+ln\left|\frac{t-1}{t+1}\right|+C=\sqrt{1+x^2}+ln\left|\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}\right|+C\)
d/ Con nguyên hàm này cũng không tính được, chắc bạn ghi nhầm đề

a) Điều kiện: \(\left\{{}\begin{matrix}4x+2>0\\x-1>0\\x>0\end{matrix}\right.\)
Hay là: \(x>1\)
Khi đó biến đổi pương trình như sau:
\(\ln\dfrac{4x+2}{x-1}=\ln x\)
\(\Leftrightarrow\dfrac{4x+2}{x-1}=x\)
\(\Leftrightarrow4x+2=x\left(x-1\right)\)
\(\Leftrightarrow x^2-5x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{5+\sqrt{33}}{2}\\x_2=\dfrac{5-\sqrt{33}}{2}\left(loại\right)\end{matrix}\right.\)
Vậy nghiệm của phương trình là: \(x=\dfrac{5+\sqrt{33}}{2}\)
b) Điều kiện: \(\left\{{}\begin{matrix}3x+1>0\\x>0\end{matrix}\right.\)
Hay là: \(x>0\)
Biến đổi phương trình như sau:
\(\log_2\left(3x+1\right)\log_3x-2\log_2\left(3x+1\right)=0\)
\(\Leftrightarrow\log_2\left(3x+1\right)\left(\log_3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\log_2\left(3x+1\right)=0\\\log_3x=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+1=2^0\\x=3^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=9\end{matrix}\right.\)
Vậy nghiệm là x = 9.

Câu 1:
\(\int\frac{sinx}{sinx+cosx}dx=\frac{1}{2}\int\frac{sinx+cosx+sinx-cosx}{sinx+cosx}dx=\frac{1}{2}\int dx-\frac{1}{2}\int\frac{cosx-sinx}{sinx+cosx}dx\)
\(=\frac{1}{2}x-\frac{1}{2}\int\frac{d\left(sinx+cosx\right)}{sinx+cosx}=\frac{1}{2}x-\frac{1}{2}ln\left|sinx+cosx\right|+C\)
\(\Rightarrow\left\{{}\begin{matrix}a=\frac{1}{2}\\b=-\frac{1}{2}\end{matrix}\right.\)
\(\int cos^2xdx=\int\left(\frac{1}{2}+\frac{1}{2}cos2x\right)dx=\frac{1}{2}x+\frac{1}{4}sin2x+C\)
\(\Rightarrow\left\{{}\begin{matrix}c=\frac{1}{2}\\d=2\end{matrix}\right.\) \(\Rightarrow I=5\)
Câu 2:
\(I=\int\left(sin\left(lnx\right)-cos\left(lnx\right)\right)dx=\int sin\left(lnx\right)dx-\int cos\left(lnx\right)dx=I_1-I_2\)
Xét \(I_2=\int cos\left(lnx\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=cos\left(lnx\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-\frac{1}{x}sin\left(lnx\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I_2=x.cos\left(lnx\right)+\int sin\left(lnx\right)dx=x.cos\left(lnx\right)+I_1\)
\(\Rightarrow I=I_1-\left(x.cos\left(lnx\right)+I_1\right)=-x.cos\left(lnx\right)+C\)
b/ \(I=\int\limits sin\left(lnx\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=sin\left(lnx\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{1}{x}cos\left(lnx\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I=x.sin\left(lnx\right)-\int cos\left(lnx\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=cos\left(lnx\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-\frac{1}{x}sin\left(lnx\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I=x\left[sin\left(lnx\right)-cos\left(lnx\right)\right]-I\)
\(\Rightarrow I=\frac{1}{2}x\left[sin\left(lnx\right)-cos\left(lnx\right)\right]|^{e^{\pi}}_1=\frac{1}{2}\left(e^{\pi}+1\right)\)
\(\Rightarrow a=2;b=\pi;c=1\)