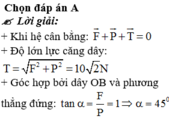Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

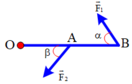
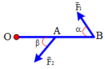
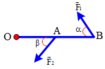
Gọi \(T\) là lực căng dây.
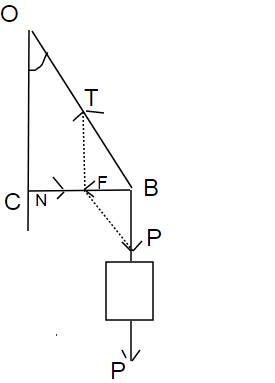
Định luật ll Niu tơn:
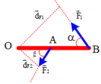
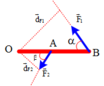
\(\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{T}=\overrightarrow{0}\)
Theo quy tắc tổng hợp lực hình bình hành:
\(\overrightarrow{P}+\overrightarrow{T}=\overrightarrow{F}\)
Mà \(\overrightarrow{F}+\overrightarrow{N}=\overrightarrow{0}\)
Theo giả thiết: \(CB=2CO\)
\(\Rightarrow tan\alpha=\dfrac{CB}{CO}=2\)\(\Rightarrow\alpha\approx63^o\)
\(cos\alpha=\dfrac{P}{T}\Rightarrow T=\dfrac{P}{cos\alpha}=\dfrac{10\cdot5}{cos63^o}=111,8N\)

a)
+ Vật cân bằng nên: 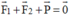 (1,50 điểm)
(1,50 điểm)
+ Chiếu phương lên trục Oy thẳng đứng ta được:
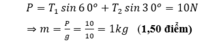
b) Theo điều kiện cân bằng của Momen lực: 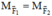
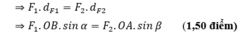
+ OB = OA + AB = 50 cm


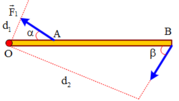
P B O C N F T P
N là phản lực cảu tường khi thanh tác dụng lực , T là lực căng của dây OB bằng trọng lực P
điều kiện để cân bằng \(\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{T}=0\)
ta có \(\overrightarrow{P}+\overrightarrow{T}=\overrightarrow{F}\)
\(\Rightarrow\)\(\overrightarrow{F}+\overrightarrow{N}=0\)
theo đề bài ta có CB=2CO
tan\(\alpha\)=\(\dfrac{CB}{CO}\)\(\Rightarrow\)\(\alpha\)=........ (ko có máy tính)
cos\(\alpha\)=\(\dfrac{P}{T}\)\(\Rightarrow\)T=P/cos\(\alpha\)=.........
ta có N=F=T.sin\(\alpha\)=........

\(OB=1,2m\)
\(\Rightarrow OA=1,5-1,2=0,3m\)
Để AB cân bằng \(\Leftrightarrow M_A=M_B\)
\(\Rightarrow m_1g\cdot OA=m_2g\cdot OB\)
\(\Rightarrow\dfrac{P_1}{10}\cdot OA=\dfrac{P_2}{10}\cdot OB\)
\(\Rightarrow\dfrac{P_1}{10}\cdot0,3=\dfrac{50}{10}\cdot1,2\)
\(\Rightarrow P_1=200N\)
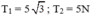 . Vật có khối lượng là bao nhiêu?
. Vật có khối lượng là bao nhiêu?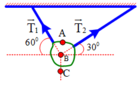
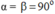 . Tính F2
. Tính F2