Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn tham khảo link này nha:
https://qanda.ai/vi/solutions/zag1U2SSkY.


a) xét
\(\Delta BME\text{VÀ}\Delta CMA\\ BM=CM\left(gt\right)\\ \widehat{BME}=\widehat{CMA}\\ MA=ME\left(gt\right)\\ \Delta BME=\Delta CMA\left(c-g-c\right)\Rightarrow BE=AC\\ \widehat{EMB}=\widehat{ACM}\left(\text{MÀ Ở VỊ TRÍ SO LE TRONG}\right)\\ \Rightarrow AC\text{//}BE\)
:V lười gõ tiếp quá ;-;
mà bạn cho mình hỏi. =) mình thấy bạn đăng toàn câu hỏi nâng cao bạn đang thi HSG hả ;-; mình 24/1 thi rồi =) không biết bạn có thi không =)))
a, xét tam giác MAC và tâm giác MEB
có{ME=MA(gt);BM=MC;tam giác MAC= tam giác MEB(c-g-c)
=> AC = EB=>EMB^=ACM^( mà ở vị trí so le trong)
=> AC// BE
b, Xét tam giác AIM và tam giác KME
có { AI=KE(gt);M3^=M4^; AM=ME(gt)
=> tam giác AIM= tam giác KME(c-g-c)
=> IM=MK
=> I,M,K thẳng hàng
c, ta có : tam giác HEB
có { H^ =90°;B^ =50°;MEB^=25°
=> H^ + B^ + MEB^ +HEM^ =180°
=> 90°+50°+25°+HEM^ =180°
=> HEM^ =180°-90°-50°-25°
=> HEM^=15°
lại có tam giác BME
{B^=50°;E^=25°
=> B^+E^+BME^= 180°
=> BME^ = 180° -25°-50°
=> BME^ =105°

Do AC=BE(gt)
AMC=BME(đối đỉnh)
BM=MC(M là trung điểm BC)
Suy ra tam giác AMC=tam giác BME(c-g-c)
ACM=MBE và hai góc này ở vị trí so le trong nên AC // BE
a/ Xét tam giác AMC và tam giác EMB có
AM=ME(gt)
góc AMC=góc EMB(đối đỉnh)
BM=MC( M là trung điểm của BC)
Vậy tam giác AMC = tam giác EMB(c-g-c)

a) CMR AC // BE
xét tam giacs AMC và tam giác EMB
có AM = ME (gt)
BM = MC (M trung điểm BC)
\(\widehat{AMC}=\widehat{EMB}\left(dd\right)\)
=> tam giác AMC = tam giác EMB (cgc)
=> \(\widehat{MBE}=\widehat{MCB}\)mà chúng ở vị trí so le trong => AC//BE
b) bạn tự thêm điểm I và K vào hình vẽ nhé, mình lười :))
ta có I thuộc AC, K thuộc BE nên
IC = AC - AI và BK = BE - KE
mà AC = BE (cmt), AI = KE (gt)
=> IC = BK
xét tam giác IMC và tam giác KMB
có: BK = IC (cmt)
BM = MC (cmt)
góc MBK = góc ICM (AC//BE)
=> tam giác IMC = tam giác KMB (cgc)
=> góc IMC = góc KMB
khi đó góc IMK = 180 độ
I, M, K thẳng hàng

a: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AC//BE

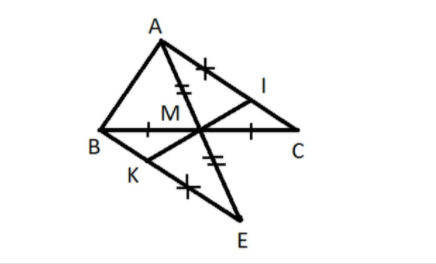
1: Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMEB
=>AC=BE
ΔMAC=ΔMEB
=>\(\widehat{MAC}=\widehat{MEB}\)
=>AC//EB
b: Xét ΔIAM và ΔKEM có
IA=KE
\(\widehat{IAM}=\widehat{KEM}\)
AM=ME
Do đó: ΔIAM=ΔKEM
=>\(\widehat{IMA}=\widehat{KME}\)
mà \(\widehat{IMA}+\widehat{IME}=180^0\)(hai góc kề bù)
nên \(\widehat{KME}+\widehat{IME}=180^0\)
=>I,M,K thẳng hàng