Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMKN có
\(\widehat{AMK}=\widehat{ANK}=\widehat{MAN}=90^0\)
=>AMKN là hình chữ nhật
b: Xét ΔABC có
K là trung điểm của BC
KM//AC
Do đó: M là trung điểm của AB
Xét ΔABC có
K là trung điểm của BC
KN//AB
Do đó: N là trung điểm của AC
Xét tứ giác AKBE có
M là trung điểm chung của AB và KE
nên AKBE là hình bình hành
Xét hình bình hành AKBE có AB\(\perp\)KE
nên AKBE là hình thoi
c: Xét tứ giác AKCF có
N là trung điểm chung của AC và KF
nên AKCF là hình bình hành
=>CF//AK và CF=AK
AKBE là hình bình hành
=>BE//AK và BE=AK
BE//AK
CF//AK
Do đó: BE=CF
BE=AK
CF=AK
Do đó: BE=CF

B A C M N E F Q
MK K QUEN VẼ TRÊN MÁY TÍNH LÊN HÌNH NÓ K ĐƯỢC CHUẨN , BẠN VẼ VOAFP VỞ THÌ CÂN CHÍNH XÁC HÔ NHÉ
bài làm
xét tám giác ABC có M là trung điểm của AB ; N là trung điểm của AC
áp dụng tc đường trung bình trong 1 tam giác ta có : MN // BC ; MN = \(\frac{1}{2}\) BC
Xét tứ giác BMNC ; có MN//BC ( cmt )
=> BMNC là thang( dn ............)
mà góc B = góc C ( tam giác ABC cân ) => BMNC là hình thang cân
có MN=\(\frac{1}{2}\) BC mà MN=6cm => BC=12
b)
có NM//BC => MN//BE (1)
có MN=\(\frac{1}{2}\)BC mà BE=\(\frac{1}{2}\) BC ( vì AE là đường trung tuyến => BE=EC=\(\frac{1}{2}\) BC )
=> MN=BE (2)
từ (1) và (2)
=> BMNE là hình bình hành ( 2 cạnh song song và = nhau)
c)
có tam giác ABC cân tại A => AB = AC
có AN=\(\frac{1}{2}AC\) ;\(AM=\frac{1}{2}AB\) mà AB=AC(cmt)
=> AN=AM
xét tứ giác AMEN có AM và AN là 2 cạnh kề mà AM=An => AMEN là hình thoi (dn............)
d)
có tam giác ABC cân tại A mà AE là đường trung tuyến => AE là đường cao => AE \(\perp BC\)
hay \(AF\perp BC\)
xét tứ giác ABFC có AF và BC là 2 đường chéo
mà \(AF\perp BC\)
=> ABFC là hình thoi (định nghĩa ......................)
e)
xét tứ giác AQCE
có AC và EQ là 2 đường chéo cắt tại N
mà N là trung điểm của AC ( đề bài )
N là trung điểm của EQ( tia đối )
=> AQCE là hình bình hành
mà AEC=900 ( vì \(AE\perp BC\left(cmt\right)\) )
=> AQCE là hình chữ nhật ( hình bình hành có 1 góc vuông là hình chữ nhật)
~~~~~~~~~~~~~~~~my love~~~~~~~~
k chắc nha , chỗ nào k hỏi add + ib hỏi mk ,

a: Xét tứ giác ABEC có
M là trung điểm chung của AE và BC
nên ABEC là hình bình hành
b: ABEC là hình bình hành
=>AC//BE và AC=BE
AC=BE
AC=AD
Do đó: BE=AD
AC//BE
=>BE//AD
Xét tứ giác ADBE có
AD//BE
AD=BE
Do đó: ADBE là hình bình hành
c: ADBE là hình bình hành
=>AB cắt DE tại trung điểm của mỗi đường
=>N là trung điểm chung của AB và DE
=>NA=NB
d: Xét ΔBAC có BM/BC=BN/BA
nên MN//AC
MN//AC
AC\(\perp\)AB
Do đó: MN\(\perp AB\)

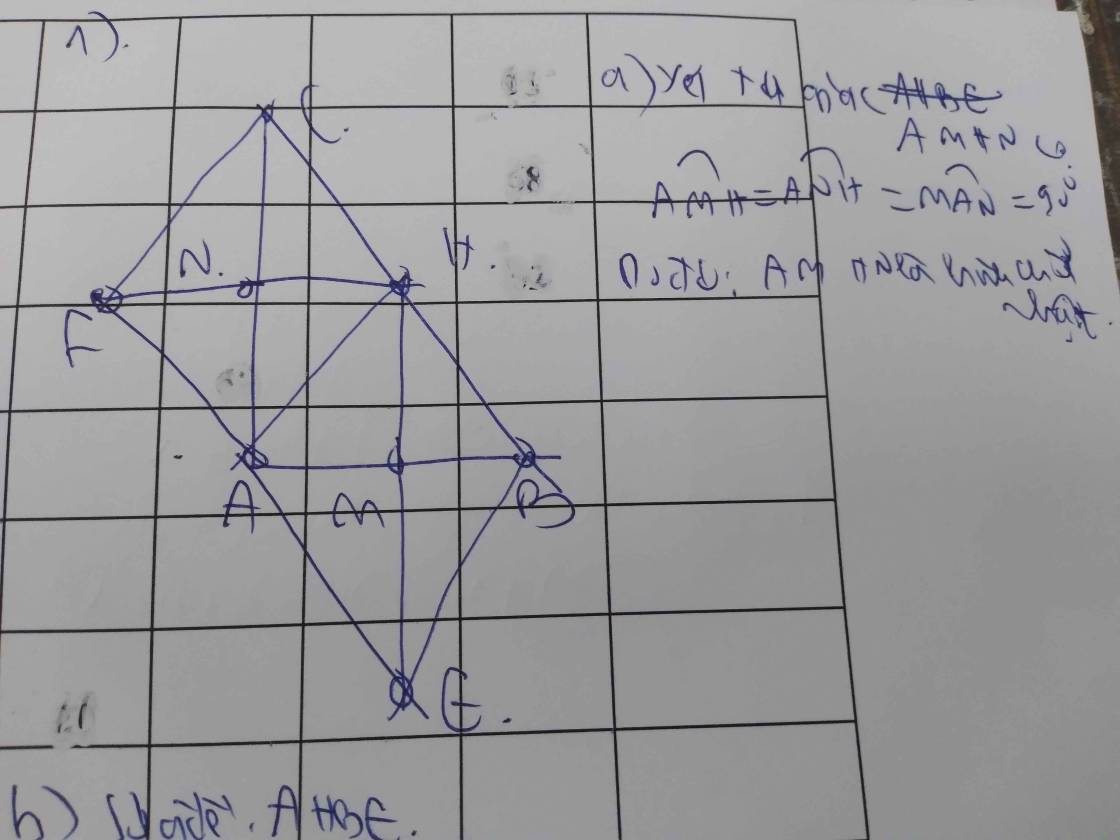
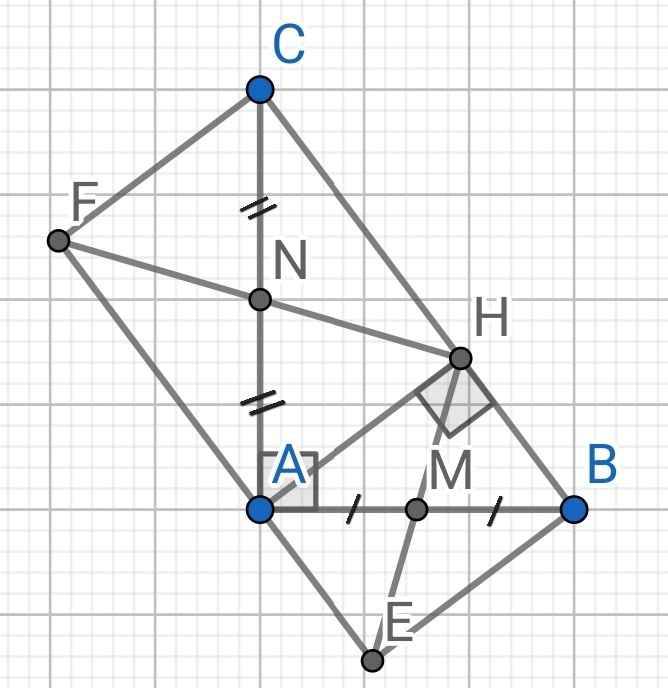 a) Do H và E đối xứng qua M (gt)
a) Do H và E đối xứng qua M (gt)
⇒ M là trung điểm HE
Tứ giác AHBE có:
M là trung điểm AB (gt)
M là trung điểm HE (cmt)
⇒ AHBE là hình bình hành
Lại có:
∠AHB = 90⁰ (AH ⊥ BC)
⇒ AHBE là hình chữ nhật
b) Do F và H đối xứng qua N
⇒ N là trung điểm của HF
Tứ giác AHCF có:
N là trung điểm AC (gt)
N là trung điểm HF (cmt)
⇒ AHCF là hình bình hành
⇒ AH = CF và AH // CF (1)
Do AHBE là hình chữ nhật (cmt)
⇒ AH // BE và AH = BE (2)
Từ (1) và (2) suy ra:
CF // BE và CF = BE

H A B C I J D E
a) \(AB\perp AC\)
\(HJ\perp AC\)
=> AB//HJ (1)
Lại có \(AC\perp AB\)
\(HI\perp AB\)
=> AC//HI (2)
Từ (1) (2) => AIHJ là hình bình hành (3)
Mà \(\widehat{A}=90^o\)=> AIHJ là hình chữ nhật
b) D đ/xứng H qua I => I là trung điểm của HD
=> HI = ID (4)
Do AB và HI vuông góc => AB là đường trung trực của HD => AD = AH (6)
E đ/xứng H qua J => J là trung điểm của HE
=> HE = EJ (5)
Do AC và HJ vuông góc => AC là đường trung trực của HE
AIHJ là hình bình hành (cm a)
=> HI = AJ
Từ (4) => HI = ID = AJ hay ID = AJ (7)
Lại có IJ = AH (trg hình bình hành hai đươờng chéo bằng nhau)
Từ (6) => IJ = DA (8)
Từ (7) (8) => DAIJ là hình bình hành
(sai thì thôi)


BE=2*BA
DC=2*AC
mà AB=AC
nên BE=DC
Xét tứ giác BCED có
A là trung điểm chung của BE và CD
Do đó: BCED là hình bình hành
Hình bình hành BCED có BE=CD
nên BCED là hình chữ nhật