
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét ΔAHE vuông tại E và ΔABD vuông tại D có
\(\widehat{EAH}\) chung
Do đó: ΔAHE\(\sim\)ΔABD(g-g)
Suy ra: \(\dfrac{AH}{AB}=\dfrac{AE}{AD}\)
hay \(AB\cdot AE=AH\cdot AD\)
b) Xét ΔEHA vuông tại E và ΔEBC vuông tại E có
\(\widehat{AHE}=\widehat{CBE}\)(ΔAHE\(\sim\)ΔABD)
Do đó: ΔEHA\(\sim\)ΔEBC(g-g)
Suy ra: \(\dfrac{EH}{EB}=\dfrac{EA}{EC}\)
hay \(EA\cdot EB=EH\cdot EC\)
d) Ta có: ΔABC cân tại A(gt)
mà AD là đường cao ứng với cạnh đáy BC(Gt)
nên AD là đường trung tuyến ứng với cạnh BC
Suy ra: \(BD=DC=\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABD vuông tại D, ta được:
\(AD^2+BD^2=AB^2\)
\(\Leftrightarrow AD^2=5^2-3^2=16\)
hay AD=4(cm)
Xét ΔBEC vuông tại E và ΔBDA vuông tại D có
\(\widehat{B}\) chung
Do đó: ΔBEC\(\sim\)ΔBDA(g-g)
Suy ra: \(\dfrac{BE}{BD}=\dfrac{BC}{BA}\)
\(\Leftrightarrow BE=\dfrac{6\cdot3}{5}=\dfrac{18}{5}=3.6\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBEC vuông tại E, ta được:
\(BC^2=BE^2+EC^2\)
\(\Leftrightarrow EC^2=6^2-3.6^2=23.04\)
hay EC=4,8(cm)

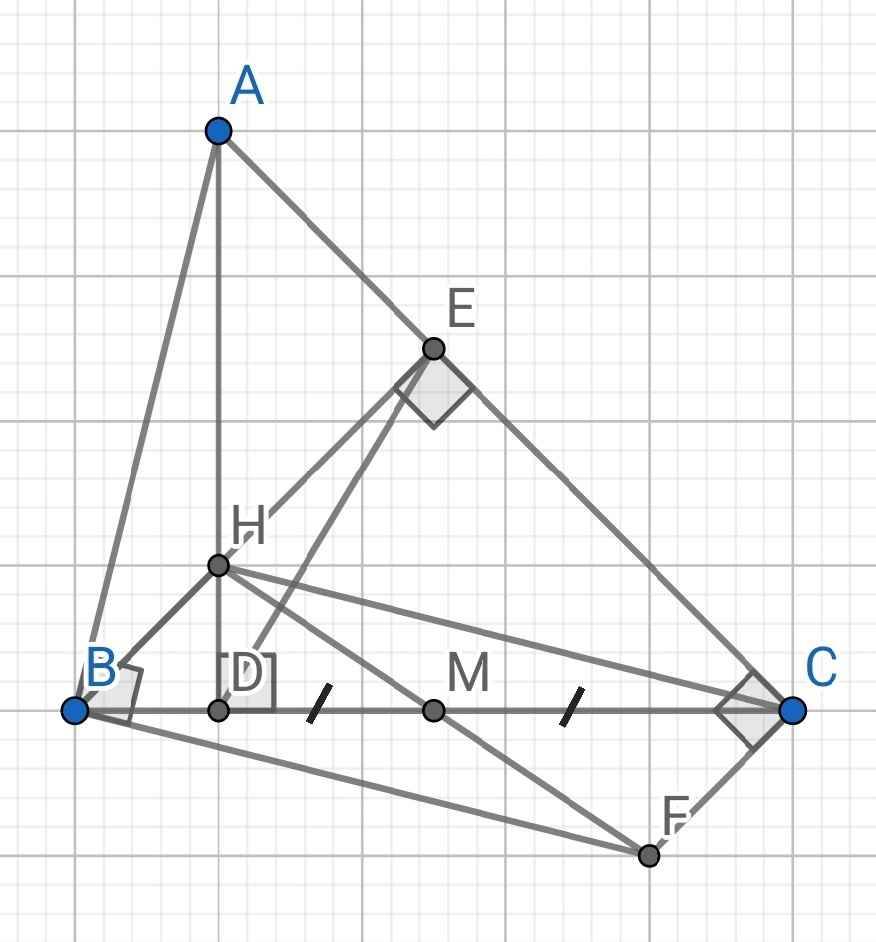 d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
⇒ CH là đường cao thứ ba của ∆ABC
⇒ CH ⊥ AB
Mà BF ⊥ AB (gt)
⇒ CH // BF
Do CF ⊥ AC (gt)
BE ⊥ AC (gt)
⇒ CF // BE
⇒ CF // BH
Tứ giác BHCF có:
CH // BF (cmt)
CF // BH (cmt)
⇒ BHCF là hình bình hành
e) Do BHCF là hình bình hành (cmt)
Mà M là trung điểm của đường chéo BC (gt)
⇒ M là trung điểm của đường chéo HF
⇒ H, M, F thẳng hàng

b: Ta có: ΔABC cân tại A
mà AD là đường cao
nên Dlà trung điểm của BC
Xét ΔCDH vuông tại D và ΔADB vuông tại D có
góc HCD=góc BAD
Do đó; ΔCDH đồng dạng với ΔADB
Suy ra: CD/AD=DH/DB
hay \(AD\cdot DH=CD^2\)

b: Ta có: ΔABC cân tại A
mà AD là đường cao
nên D là trung điểm của BC
Xét ΔBDA vuông tại D và ΔHDC vuông tại D có
góc DBA=góc DHC
DO đó: ΔBDA đồng dạng với ΔHDC
Suy ra: DB/DH=DA/DC
hay \(DH\cdot DA=DB\cdot DC=DC^2\)

a: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có
góc C chung
=>ΔCDA đồng dạng với ΔCEB
=>CD/CE=CA/CB
=>CD/CA=CE/CB; CD*CB=CA*CE
b: Xét ΔCDE và ΔCAB có
CD/CA=CE/CB
góc C chung
=>ΔCDE đồng dạng với ΔCAB
c: góc BEC=góc BFC=90 độ
=>BFEC nội tiếp
=>góc AEF=góc ABC=góc DEC

Xét ΔABC có
BE là đường phân giác ứng với cạnh AC
nên \(\dfrac{AE}{EC}=\dfrac{AB}{BC}\left(1\right)\)
Xét ΔABC có
CD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AC}{BC}\left(2\right)\)
Ta có: ΔBAC cân tại A
nên \(AB=AC\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
hay DE//BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
mà \(\widehat{DBC}=\widehat{ECB}\)
nên BDEC là hình thang cân
Xét ΔEDC có \(\widehat{EDC}=\widehat{ECD}\left(=\widehat{DCB}\right)\)
nên ΔEDC cân tại E
Suy ra: ED=EC=BD

a) Ta có: AE//BF vì cung vuông góc CD
AB//CD// EF (E,F thuộc CD)
=> ABFE là hình bình hành
=> AE=EF
b) Gọi I là tđ AB, K là tđ CD
=> IK vuông góc AB,CD vì ABCD là hình thang cân
Vì đường chéo hình thang cân cắt nhau tại 1 điểm chắc chắn thuộc IK( Tính chất hình thang cân)
=> KI//AE//BF
Mà CF = DE
=> K cũng là trung điểm CD
=> MJ//AE//BE
Đúng thì tim giúp nha bạn. Thx

a) Xét \(\Delta ABD\)và \(\Delta CBF\)có:
\(\widehat{ADB}=\widehat{CFB}\left(=90^0\right)\).
\(\widehat{ABC}\)chung.
\(\Rightarrow\Delta ABD~\Delta CBF\left(g.g\right)\)(điều phải chứng minh).
Vì \(\Delta ABC\)cân tại \(A\)\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
Xét \(\Delta BCE\)vuông tại \(E\)và \(\Delta CBD\)vuông tại \(D\), có :
\(\hept{\begin{cases}BC:chung\\\widehat{ACB}=\widehat{ABC}\end{cases}}\)
\(\Rightarrow\Delta BCE=\Delta CBD\left(ch.gn\right)\)
\(\Rightarrow CE=BD\)(2 cạnh tương ứng )
Vậy \(BD=CE\)