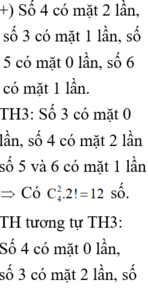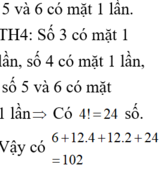Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chữ số hàng đơn vị có 5 cách chọn
Xếp 5 chữ số còn lại sao cho không có 2 chữ số 2 nào đứng cạnh nhau có đúng 1 cách dạng 2x2y2 trong đó x;y là chữ số bất kì khác được chọn từ 8 chữ số còn lại
Số số thỏa mãn: \(5.A_8^2=...\)
Chọn A
Cách 1:
Ta có S là tập hợp các số tự nhiên gồm 9 chữ số được lập từ X = {6;7;8}, trong đó chữ số 6 xuất hiện 2 lần; chữ số 7 xuất hiện 3 lần; chữ số 8 xuất hiện 4 lần nên
Có cách xếp 2 chữ số 6 vào 2 trong 9 vị trí
Có cách xếp 3 chữ số 7 vào 3 trong 7 vị trí còn lại
Có 1 cách xếp 4 chữ số 8 vào 4 trong 4 vị trí còn lại
Chọn ngẫu nhiên một số từ tập S nên 
Gọi A là biến cố “số được chọn là số không có chữ số 7 đứng giữa hai chữ số 6”
TH1: 2 chữ số 6 đứng liền nhau
Có 8 cách xếp cho số .Trong mỗi cách như vậy có C 7 3 cách xếp chữ số 7 và 1 cách xếp cho các chữ số 8
Vậy có số 8. C 7 3 .1 = 280 số
TH2: Giữa hai số 6 có đúng 1 chữ số và số đó là số 8.
Có 7 cách xếp cho số .Trong mỗi cách như vậy có C 6 3 cách xếp chữ số 7 và 1 cách xếp các chữ số 8
Vậy có 7. C 6 3 = 140 số
TH3: Giữa hai số 6 có đúng 2 chữ số và đó là hai chữ số 8.
Tương tự Có 6. C 5 3 = 60 số
TH4: Giữa hai số 6 có đúng 3 chữ số và đó là ba chữ số 8.
Có 5. C 4 3 = 20 số
TH5: Giữa hai số 6 có đúng 4 chữ số và đó là bốn chữ số 8.
Có 4. C 4 3 = 4 số
Từ đó suy ra 
Xác suất cần tìm là 
Cách 2:
- Số phần tử không gian mẫu 
- Tính số phần tử của biến cố A“số được chọn là số không có chữ số 7 đứng giữa hai chữ số 6”
Xếp 2 số 6 có 1 cách: 
Xếp 3 số 7 vào 2 khoảng 
cách ( số cách xếp bằng số nghiệm nguyên không âm của phương trình 
Xác suất cần tìm là 
Chọn C
Ta có thể chia làm bốn trường hợp sau
TH1: Số 5 có mặt một lần, số 6 có mặt một lần.( Bao gồm các khả năng sau: mỗi số có mặt một lần hoặc một số 5, một số 6 hai số 3 hoặc một số 5, một số 6 hai số 4)
Số các số được tạo thành là: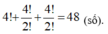 
TH2: Số 5 có mặt một lần, số 6 không có mặt.
Số các số được tạo thành là: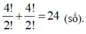 
TH3: Số 6 có mặt một lần, số 5 không có mặt.
Số các số được tạo thành là: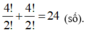 
TH4: Số 5 và số 6 không có mặt.( Số 3 và số 4 mỗi số có mặt đúng hai lần)
Số các số được tạo thành là: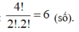 
Vậy có thể lập được 102 số thỏa mãn đề bài.
Chọn 5 chữ số từ 9 chữ số còn lại và hoán vị chúng: \(A_9^5\) cách
5 chữ số đã cho tạo thành 6 khe trống, xếp 3 chữ số 1 vào 6 khe trống đó: \(C_6^3\) cách
\(\Rightarrow A_9^5.C_6^3\) số (bao gồm cả trường hợp số 0 đứng đầu)
Chọn 5 chữ số, trong đó có mặt chữ số 0: \(C_8^4\) cách
Xếp 5 chữ số sao cho số 0 đứng đầu: \(4!\) cách
5 chữ số (trong đó vị trí 0 đứng đầu cố định) tạo ra 5 khe trống, xếp 3 chữ số 1 vào 5 khe trống đó: \(C_5^3\) cách
\(\Rightarrow\) Tổng cộng có: \(A_9^5.C_6^3-C_8^4.4!.C_5^3\) số thỏa mãn
Số số thỏa mãn: \(\dfrac{9!}{5!}=3024\) số
(Đây là loại hoán vị lặp)
a. Không gian mẫu của phép thử gồm 5 phần tử được mô tả sau:
Ω = {S, NS, NNS, NNNS, NNNN}
b. Xác định các biến cố:
+ A: "Số lần gieo không vượt quá 3"
A = {S, NS, NNS}
+ B: "Số lần gieo là 4"
B = {NNNS, NNNN}.
Số chữ số tìm được là \(\dfrac{C^2_5\cdot5!}{3!}=200\)
Số số chia hết cho 3 là \(\dfrac{2\cdot5!}{3!}=40\)
\(\Rightarrow P=\dfrac{40}{200}=\dfrac{1}{5}\)