Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do A⊂BA⊂B nên nếu X⊂A⇒X⊂BX⊂A⇒X⊂B
Do đó ta chỉ cần tìm tập còn của tập A
Tập con của A gồm: ∅;{1};{2};{1;2}∅;{1};{2};{1;2} có 4 tập thỏa mãn

Các tập X:
\(\left\{1;2\right\};\left\{1;2;3\right\};\left\{1;2;4\right\};\left\{1;2;5\right\};\left\{1;2;3;4\right\};\left\{1;2;3;5\right\};\left\{1;2;4;5\right\};\left\{1;2;3;4;5\right\}\)

a/ \(\left\{1;2\right\};\left\{1;2;3\right\};\left\{1;2;4\right\};\left\{1;2;5\right\};\left\{1;2;3;4;5\right\}\)
b/ \(\left\{1;2;3;4\right\}\)

\(x=\left\{a,b,40,41\right\}\) hoặc \(x=\left\{a,b,40,42\right\}\)

\(\left\{{}\begin{matrix}X\subset A\\X\subset B\end{matrix}\right.\) \(\Leftrightarrow X\subset\left(A\cap B\right)\)
\(A\cap B=\left\{1;2\right\}\)
\(\Rightarrow\) Các tập X thỏa mãn là \(\varnothing;\left\{1\right\};\left\{2\right\};\left\{1;2\right\}\) có 4 tập

A hợp X=B
=>X={1;3;4;0}; X={1;3;4;2}; A={1;3;4;0;2}
=>Có 3 tập hợp X thỏa mãn yêu cầu

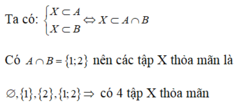
Do \(A\subset B\) nên nếu \(X\subset A\Rightarrow X\subset B\)
Do đó ta chỉ cần tìm tập còn của tập A
Tập con của A gồm: \(\varnothing;\left\{1\right\};\left\{2\right\};\left\{1;2\right\}\) có 4 tập thỏa mãn