Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
gọi số cần tìm là abcdef (a#0 ; a;b;c;d;e;f € A ; f chẵn )
f có 3 cách chọn
a có 5 cách chọn lọc
b;c;d;e đều có 6 cách chọn
=> có 3*5*6*6*6*6 = 19440 số thỏa mãn yêu cầu bài toán
b) gọi số cần tìm là abcdef (a#0;f=0,5 ; a;b;c;d;e;f € A )
f=0,5 => f có 2 cách chọn
a có 5 cách chọn
b;c;d;e đều có 6 cách chọn
=> có 2*5*6*6*6*6 = 12960
Chọn C
Số có bốn chữ số có dạng : a b c d ¯
( a≠0,a,b,c,d∈ E={0,1,2,3,4,5})
Do a b c d ¯ không chia hết cho 5 nên có 4 cách chọn d( là 1,2,3,4)
Chọn a ∈ E\{0,d} nên có 4 cách chọn a
Chọn b ∈ E\{a,d} nên có 4 cách chọn b
Chọn c ∈ E\{a,b,d} nên có 3 cách chọn c
Theo quy tắc nhân, có 4*4*4*3=192 số
Số tự nhiên đó có dạng \(\overline{abcde}\)
a, a có 5 cách chọn.
b có 5 cách chọn.
c có 4 cách chọn.
d có 3 cách chọn.
e có 2 cách chọn.
\(\Rightarrow\) Có \(5.5.4.3.2=600\) số thỏa mãn.
b, TH1: \(e=0\)
a có 5 cách chọn.
b có 4 cách chọn.
c có 3 cách chọn.
d có 2 cách chọn.
\(\Rightarrow\) Có \(5.4.3.2=120\) số thỏa mãn.
TH2: \(e\ne0\)
a có 5 cách chọn.
e có 2 cách chọn.
b có 4 cách chọn.
c có 3 cách chọn.
d có 2 cách chọn.
\(\Rightarrow\) Có \(5.4.3.2.2=240\) số thỏa mãn.
Vậy có \(120+240=360\) số tự nhiên thỏa mãn yêu cầu bài toán.
c, TH1: \(e=0\Rightarrow\) có 120 số thỏa mãn.
TH2: \(e=5\)
a có 4 cách chọn.
b có 4 cách chọn.
c có 3 cách chọn.
d có 2 cách chọn.
\(\Rightarrow\) Có \(4.4.3.2=96\) số thỏa mãn.
Vậy có \(120+96=216\) số tự nhiên thỏa mãn yêu cầu bài toán.
Chọn C
Giả sử số lập được có dạng 
Ta có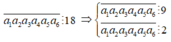 
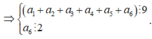
Vì 
nên ta có các trường hợp sau
Trường hợp 1:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ 
+ Có 3 cách chọn chọn a 6
+ Có 5! cách chọn chọn bộ 5 số 
Suy ra có 3.5! = 360 số.
Trường hợp 2:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ 
+
a
6
= 0, có 5! cách chọn bộ 5 số 
+
a
6
≠
0 khi đó
a
6
có 3 cách chọn,
a
1
có 4 cách chọn và có 4! cách chọn bộ 4 số 
Suy ra có 5! + 3.4.4!= 408 số
Trường hợp 3:
a
1
,
a
2
,
a
3
,
a
4
,
a
5
,
a
6
được chọn từ 
+
a
6
= 0, có 5! cách chọn bộ 5 số 
+
a
6
≠
0 khi đó
a
6
có 1 cách chọn,
a
1
có 4 cách chọn và có 4! cách chọn bộ 4 số 
Suy ra có 5! + 1.4.4! = 216 số
Vậy có: 360 + 408 + 216 = 984 số.
\(\overline{abcdef}\)
TH1: f=0
=>Có 8*7*6*5*4=6720 cách
TH2: f=5
=>Có 7*7*6*5*4=5880 cách
=>Có 6720+5880=12600 cách
Có 5 cách chọn chữ số hàng trục nghìn
Có 5 cách chọn chữ số hàng nghìn
Có 5 cách chọn chữ số hàng trăm
Có 5 cách chọn chữ số hàng trục
Có 5 cách chọn chữ số hàng đơn vị
=> Có thể lập được bao nhiêu số tự nhiên có 5 chữ số từ các số đã cho là:
5.5.5.5.5 = 3125 ( số )
TH1: f=0
=>Có 8*7*6*5*4=6720 cách
TH2: f=5
=>Có 7*7*6*5*4=5880 cách
=>Có 6720+5880=12600 cách