Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hai cạnh góc vuông đó có độ dài là (8cm)và (6cm)
mình nghĩ như vậy nếu sai bạn thông cảm nha !!!
chúc bạn học tốt
Gọi 2 cạch góc vuông của tam giác lần lượt là a,b :
Ta có : Hai cạch góc vuông hơn kém nhau 2 cm
=> a - b = 2 ( 1 )
Áp dụng định lý pi - ta - go vào tam giác ta đc :
a^2+b^2=10^2(2)
Từ ( 1 ) và ( 2 ) suy ra :
+) a = b+2 thay vào : ( b + 2 )^2 + b^2 = 100
<=> 2b^2 + 4b -96 = 0
=> b=6 ( t/m )hoặc b=8 ( loại )
=> b = 6
=> a =8
Vậy : S = 1/2 .6 . 8 = 24

Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
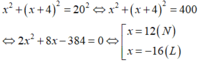
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm

Phương trình hoành độ giao điểm của (P) và (d) là \(x^2=mx-m+1\)\(\Leftrightarrow x^2-mx+m-1=0\)
Để (d) cắt (P) tại 2 điểm phân biệt thì \(\Delta=\left(-m\right)^2-4.1\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2>0\)\(\Leftrightarrow m-2\ne0\)\(\Leftrightarrow m\ne2\)
Khi đó \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-1\end{cases}}\)(hệ thức Vi-ét)
Độ dài cạnh huyền của tam giác vuông có 2 cgv là \(x_1,x_2\)là \(\sqrt{x_1^2+x_2^2}=\sqrt{\left(x_1+x_2\right)^2-2x_1x_2}=\sqrt{m^2-2\left(m-1\right)}=\sqrt{m^2-2m+2}\)
Ta có \(x_1x_2=\frac{1}{\sqrt{5}}\sqrt{m^2-2m+2}\)hệ thức lượng trong tam giác vuông.
\(\Leftrightarrow m-1=\frac{1}{\sqrt{5}}\sqrt{m^2-2m+2}\)\(\Leftrightarrow\frac{m-1}{\sqrt{m^2-2m+2}}=\frac{1}{\sqrt{5}}\)\(\Leftrightarrow\sqrt{\frac{m^2-2m+1}{m^2-2m+2}}=\sqrt{\frac{1}{5}}\)\(\Leftrightarrow\frac{m^2-2m+1}{m^2-2m+2}=\frac{1}{5}\)\(\Leftrightarrow5m^2-10m+5=m^2-2m+2\)\(\Leftrightarrow4m^2-8m+3=0\)
\(\Delta_1=\left(-8\right)^2-4.4.3=16>0\)
\(\Rightarrow\orbr{\begin{cases}m_1=\frac{-\left(-8\right)+\sqrt{16}}{2.4}=\frac{3}{2}\\m_2=\frac{-\left(-8\right)-\sqrt{16}}{2.4}=\frac{1}{2}\end{cases}}\)
Vậy để [...] thì \(\orbr{\begin{cases}m=\frac{3}{2}\\m=\frac{1}{2}\end{cases}}\)

Bài 1) Vì B = 30°
=》sinB = 1/2 (tính chất )
=》cosB = \(\sqrt{ }\)3/2 ( tính chất )
=》 tanB = \(\sqrt{ }\)3/3( tính chất )
=》 cotB = \(\sqrt{ }\)3( tính chất )
Lại có B + C = 90°
=》 sinB = cosC = 1/2
=》 cosB = sinC = \(\sqrt{ }\)3/2
=》tanB = cotC = \(\sqrt{ }\)3/3
=》cotB = tanC = \(\sqrt{ }\)3
SinA = BC/BC = 1
CosA có thể bằng AB/BC hay AC/BC (loại)
TanA có thể bằng BC/AB hay BC/AC (loại)
CotA có thể bằng AB/BC hay AC/BC (loại)
Bài 2) Vì \(\Delta\)MNP vuông cân tại M
=》 MN = MP = b
Áp dụng định lý Py ta go vào \(\Delta\)ABC có :
NM2 +MP2 = NP2
=》 NP2 =b2 + b2 =2b2
=》NP = \(\sqrt{ }\)2b2
SinN = MP/NP = b/\(\sqrt{ }\)2b2 = \(\sqrt{ }\)2/2
CosN = NM/NP = b/\(\sqrt{ }\)2b2 = \(\sqrt{ }\)2/2
TanN = MP/NM = b/b =1
CotN = NM/MP = b/b = 1
Vì N + P =90°
=》sinN = cosP = \(\sqrt{ }\)2/2
=》cosN = sinP =\(\sqrt{ }\)2/2
=》tanN = cotP = 1
=》cotN = tanP = 1

gọi 2 canh tam giác là x và x+2
áp dụng định lí pytago ta có
x^2+(x+2)^2=10^2
suy ra x^2+x^2+4x+4=100
suy ra x=6 (vì x>0)
suy ra2 cạnh góc vuông là 6 và 8cm

NA/BA = NC/BC
Vì Tam giác ABC vuông tại A, biết AB=3cm,BC=5cm => AC= 4(cm)
=> NC-NA=4 (cm)
=> NC/BC = NA/BA = ( NC-NA)/(BC-AB) = 2
=> NA= BA*2 =6 (cm)


Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm