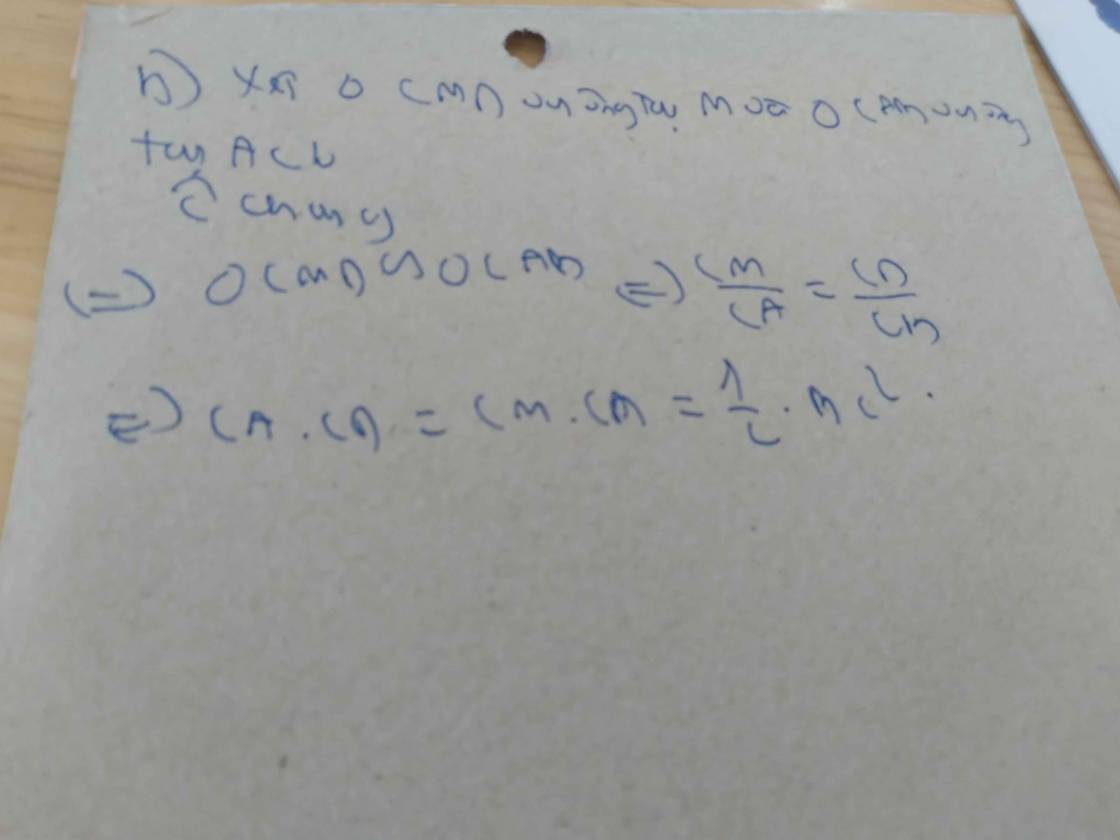Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,
Do MD là trung trực của BC \(\Rightarrow DB=DC\)
\(\Rightarrow\Delta DBC\) cân tại D
\(\Rightarrow\widehat{DBC}=\widehat{DCB}\)
Lại có \(\widehat{BDE}=\widehat{DCB}+\widehat{DBC}=2\widehat{DCB}=2\widehat{ACB}\) (góc ngoài của tam giác) (1)
Do \(\left\{{}\begin{matrix}AB\perp DE\left(gt\right)\\AE=AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AB\) là trung trực DE
\(\Rightarrow BE=BD\Rightarrow\Delta BDE\) cân tại B \(\Rightarrow\widehat{BEC}=\widehat{BDE}\) (2)
(1);(2) \(\Rightarrow\widehat{BEC}=2\widehat{ACB}\)
b.
Xét hai tam giác BAC và DMC có:
\(\left\{{}\begin{matrix}\widehat{C}\text{ chung}\\\widehat{BAC}=\widehat{DMC}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta BAC\sim\Delta DMC\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{MC}=\dfrac{BC}{CD}\Rightarrow CA.CD=BC.MC=BC.\dfrac{1}{2}BC=\dfrac{BC^2}{2}\)

a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành
B A C D E K

2/. Tam giác AKC có
CH là đường cao
AE là đường cao
Ch cắt AE tại E
Nên E là trực tâm của tam giác AKC
3/. Ta có góc HAC + góc HCA = 90 độ
Ta có góc IEC + góc ECI = 90 độ => góc ICE + góc HCA = 90 độ
=> góc HAC = góc IEC (1)
Ta có IH = AH (tam giác AIK vuông tại I, HI là trung tuyến)
=> tam giác AHI cân tại H => góc HAI = góc HIA => góc HAC = góc HIA (2)
Ta có IM = MẸ (tam giác EIC vuông tại I, IM là trung tuyến
=> tam giác EMI cân tại M => góc IEM = góc MIE => góc IEC = góc MIE (3)
Từ (1)(2)(3) ta suy ra góc HIA = góc MIE (4)
Ta có góc HIA + góc HIE = 90 độ(5)
góc HIE + góc EIM = 90 độ(6)
Từ (4)(5)(6) ta suy ra góc HIE + góc EIM = 90 độ => HI vuông góc với IM

a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
nên ADME là hình chữ nhật
b: Xét tứ giác AMBP có
D là trung điểm chung của AB và MP
MA=MB
Do đó: AMBP là hình thoi
=>ABlà phân giác của góc MAP(1)
c: Xét tứ giác AMCQ có
E là trung điểm chung của AC và MQ
MA=MC
Do đó: AMCQ là hình thoi
=>AC là phân giác của góc MAQ(2)
Từ (1), (2) suy ra góc PAQ=2*90=180 độ
=>P,A,Q thẳng hàng
mà AP=AQ
nên A là trung điểm của PQ

Bài 1:
a: Ta có: D và E đối xứng nhau qua AB
nên AD=AE
=>ΔADE cân tại A
mà AB là đường cao
nên AB là phân giác của góc EAD(1)
Ta có: D và F đối xứng nhau qua AC
nên AD=AF
=>ΔADF cân tại A
=>AC là phân giác của góc DAF(2)
Từ (1) và (2) suy ra góc EAF=2xgóc BAC=120 độ
AE=AD
AF=AD
Do đó: AE=AF
b: Xét ΔADM và ΔAEM có
AD=AE
góc DAM=góc EAM
AM chung
DO đó: ΔADM=ΔAEM
SUy ra: góc ADM=góc AEM(3)
Xét ΔADN và ΔAFN có
AD=AF
góc DAN=góc FAN
AN chung
Do đó; ΔADN=ΔAFN
Suy ra: góc ADN=góc AFN(4)
Từ (3) và (4) suy ra góc ADM=góc ADN
hay DA là phân giác của góc MDN