Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tam giác ABH vuông tại H ( AH vuong goc BC) \(\Rightarrow\) \(AB^2=BH^2+AH^2\left(pytago\right)\)
tg AHC vuông tại H \(\Rightarrow AC^2=AH^2+HC^2\)
CÓ \(AB^2+CH^2=BH^2+AH^2+CH^2\) (1)
VÀ \(AC^2+BH^2=AH^2+HC^2+BH^2\) (2)
TỪ (1),(2) \(\Rightarrow\) \(AB^2+CH^2=AC^2+BH^2\)

BTS là cục cứt chó j , nó đéo xứng làm cục cứt của the coconut tao
con kia là đồ giả mạo
Mà ông Duy có j hay đâu mà bọn m giả lắm thế

a) Chứng minh ΔBHC=ΔCKB
Xét ΔBHC vuông tại H và ΔCKB vuông tại K có
BC là cạnh chung
\(\widehat{HCB}=\widehat{KBC}\)(\(\widehat{ACB}=\widehat{ABC}\), H∈AC, K∈AB)
Do đó: ΔBHC=ΔCKB(cạnh huyền-góc nhọn)
b)
*Chứng minh IB=IC
Ta có: ΔBHC=ΔCKB(cmt)
⇒\(\widehat{HBC}=\widehat{KCB}\)(hai góc tương ứng)
hay \(\widehat{IBC}=\widehat{ICB}\)
Xét ΔIBC có \(\widehat{IBC}=\widehat{ICB}\)(cmt)
nên ΔIBC cân tại I(định lí đảo của tam giác cân)
⇒IB=IC(đpcm)
*Chứng minh \(\widehat{IBK}=\widehat{ICH}\)
Ta có: \(\widehat{ABH}+\widehat{HBC}=\widehat{ABC}\)(tia BH nằm giữa hai tia BA,BC)
\(\widehat{ACK}+\widehat{BCK}=\widehat{ACB}\)(tia CK nằm giữa hai tia CA,CB)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
và \(\widehat{HBC}=\widehat{KCB}\)(cmt)
nên \(\widehat{ABH}=\widehat{ACK}\)
hay \(\widehat{IBK}=\widehat{ICH}\)(đpcm)
c) Chứng minh KH//BC
Ta có: ΔBKC=ΔBHC(cmt)
⇒KB=HC(hai cạnh tương ứng)
Ta có: AK+KB=AB(A,K,B thẳng hàng)
AH+HC=AC(do A,H,C thẳng hàng)
mà AB=AC(ΔABC cân tại A)
và KB=HC(cmt)
nên AK=AH
Xét ΔAKH có AK=AH(cmt)
nên ΔAKH cân tại A(định nghĩa tam giác cân)
⇒\(\widehat{AKH}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy trong ΔAKH cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
⇒\(\widehat{ABC}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AKH}=\widehat{ABC}\)
mà \(\widehat{AKH}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị
nên KH//BC(dấu hiệu nhận biết hai đường thẳng song song)
A B C H K I a.Do △ABC cân ⇒∠ABC=∠ACB
Xét △BHC= △CKB (cạnh huyền-góc nhọn)
⇒∠IBC=∠ICB (2 góc tương ứng)
b. Do ∠IBC =∠ICB (câu a)
⇒△IBC cân ⇒ IB=IC
Xét △IBK=△ICH (cạnh huyền-góc nhọn)
⇒∠IBK=∠ICH (2 góc tương ứng)
c. Do △BHC=△CKB (câu a)
⇒ BH=CK (2 cạnh tương ứng)
⇒HC=KB ( 2 cạnh tương ứng)
Xét △BHK=△CKH(c.c.c)
⇒ ∠BHK=∠CKH (2 góc tương ứng)
Xét △IKH có: ∠2IHK=1800 -∠ KIH
Xét △IBC có : ∠2IBC=1800 -∠ ICB -∠BIC
Mà ∠BIC=∠KIH (2góc đối đỉnh)
⇒∠2IBC=1800-∠KIH
⇒∠IBC=∠IHK
Mà ∠IBC và ∠IHK là 2 góc so le trong
⇒KH // BC
Còn câu d thì hình như bị thiếu dữ kiện nên mik chưa làm
Chúc bn hok tốt

a )
Xét : \(\Delta ABHva\Delta ADH,co:\)
\(\widehat{H_1}=\widehat{H_2}=90^o\left(gt\right)\)
BH = HD ( gt )
AH là cạnh chung
Do do : \(\Delta ABH=\Delta ADH\left(c-g-c\right)\)
b )
Ta có : \(\Delta ABD\) là tam giác đều ( cmt )
= > \(\widehat{BAD}=60^o\) ( trong tam giác đều mỗi góc bằng 60o )
Ta có : \(\widehat{CAD}=\widehat{BAC}-\widehat{BAD}=90^o-60^o=30^o\) ( tia AD nằm giữa 2 tia AB và AC )
Hay : \(\widehat{EAD}=30^o\left(E\in AC\right)\)
Ta có :\(\widehat{ADH}=60^o\) ( \(\Delta ABD\) là tam giác đều )
Ta có : \(\widehat{HAD}=\widehat{H_2}-\widehat{ADH}=90^o-60^o=30^o\)
Ta có : \(AH\perp BC\) và \(ED\perp BC\)
= > \(AH//ED\) ( vì cùng vuông góc với BC )
=> \(\widehat{HAD}=\widehat{ADE}=30^o\) ( 2 góc so le trong của AH//ED )
=> \(\Delta AED\) là tam giác cân , và cân tại E ( vì có 2 góc ở đáy bằng nhau ( \(\widehat{HAD}=\widehat{ADE}=30^o\)) )
c ) mình không biết chứng minh AH = HF = FC nha , mình chỉ chứng minh \(\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{AH^2}\) thôi nha :
Ta có : \(\Delta ABC\) vuông tại A và AH là đường cao ( gt )
= > \(\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{AH^2}\) ( hệ thức lượng trong tam giác vuông )
Hình mình vẽ hơi xấu , thông cảm nha
HỌC TỐT !!!
a) Tam giác ABC có AH là đường cao đồng thời là trung tuyến ( BH=HD)
\(\rightarrow\) tam giác ABD cân tại A
Mà \(\widehat{B}\) = 60 độ \(\rightarrow\) tam giác ABD đều
b) Tam giác ABD đều nên \(\widehat{ADB}\) = \(\widehat{BAD}\) = 60 độ
\(\rightarrow\) \(\widehat{ADE}\) = \(\widehat{HDE}\) - \(\widehat{ADB}\) = 30 độ
Tương tự có \(\widehat{DAE}\) = 30độ
\(\Rightarrow\) Tam giác ADE cân tại E
c1) Xét tam giác AHC và tam giác CFA
\(\widehat{ACF}\) = \(\widehat{CAF}\) = 30độ
AC chung
\(\rightarrow\) tam giác bằng nhau ( cạnh huyền - góc nhọn)
\(\rightarrow\) AH = FC
Ta có \(\widehat{BAD}\) = 60 độ và \(\widehat{BAH}\) = 30 độ
\(\rightarrow \) \(\widehat{HAD}\) = 30 độ hay \(\widehat{HAF}\) = 30 độ
____Phần còn lại cm tam giác HAF cân là ra
Mk bận chút việc nên ms làm đến đây thui nka ~

Câu 1
a.
Xét \(\Delta ABC\) có :
\(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^o\) ( định lý tổng 3 góc của 1 \(\Delta\) )
\(\Rightarrow\widehat{BCA}=40^o\) (1)
Ta có Ax là tia đối của AB
suy ra \(\widehat{BAC}+\widehat{CAx}=180^o\)
\(\widehat{CAx}=80^o\)
lại có Ay là tia phân giác \(\widehat{CAx}\)
\(\Rightarrow\widehat{xAy}=\widehat{yAc}=\dfrac{\widehat{CAx}}{2}=\dfrac{80^o}{2}=40^o\) (2)
Từ (1)(2) suy ra \(\widehat{yAc}=\widehat{ACB}=40^o\)
mà chúng ở vị trí so le trong
\(\Rightarrow\) Ay//BC
Bài 2
Rảnh làm sau , đến giờ học rồi .

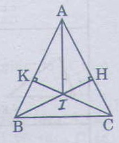
a) Hai tam giác vuông ABH và ACK có:
AB = AC(gt)
Góc A chung.
nên ∆ABH = ∆ACK(Cạnh huyền- Góc nhọn)
suy ra AH = AK.
b) Hai tam giác vuông AIK và AIH có:
AK = AH(cmt)
AI cạnh chung
Nên ∆AIK = ∆AIH(cạnh huyền- cạnh góc vuông)
Suy ra ˆIAKIAK^=ˆIAHIAH^
Vậy AI là tia phân giác của góc A.
a) Hai tam giác vuông ABH và ACH có:
Tam giác ABC cân tại A ⇒ AB = AC
AH cạnh chung.
Nên ∆ABH = ∆ACH(Cạnh huyền – cạnh góc vuông)
Suy ra HB = HC
b)∆ABH = ∆ACH (Câu a)
Suy ra ∠BAH = ∠CAH (Hai góc tương ứng)
Hãy tick câu trả lời của mk nếu bạn ko mún tick
nếu mún tick thì cứ tick
Bn biết lm k giúp mình với!!!!!!!!!