Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
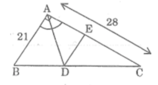
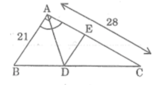
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 21 2 + 28 2 = 1225
Suy ra: BC = 35 (cm)
Vì AD là đường phân giác của ∠ (BAC) nên:
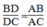(t/chất đường phân giác)
Suy ra: 
Hay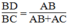 
Suy ra: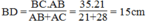 
Vậy DC = BC – BD = 35 – 15 = 20cm
Trong ΔABC ta có: DE // AB
Suy ra: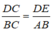 
(Hệ quả định lí Ta-lét)
Suy ra: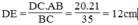 
Ta có: S A B C = 1/2.AB.AC = 1/2.21.28 = 294 ( c m 2 )
Vì △ ABC và △ ADB có chung đường cao kẻ từ đỉnh A nên:
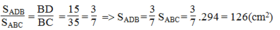
Vậy S A D C = S A B C - S A B D = 294 – 126 = 168( c m 2 )
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2=AB2+AC2=212+282=1225BC2=AB2+AC2=212+282=1225
Suy ra: BC = 35 (cm)
Vì AD là đường phân giác của ∠∠(BAC) nên:
(t/chất đường phân giác)
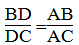
Suy ra: 
Hay 
Suy ra: 
Vậy DC = BC – BD = 35 – 15 = 20cm
Trong ΔABC ta có: DE // AB
Suy ra: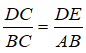 
(Hệ quả định lí Ta-lét)
Suy ra: 
a: BC=35(cm)
Xét ΔABC có AD là đường phân giác
nên BD/AB=CD/AC
hay BD/21=CD/28
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{21}=\dfrac{CD}{28}=\dfrac{BD+CD}{21+28}=\dfrac{35}{49}=\dfrac{5}{7}\)
Do đó: BD=15(cm); CD=20(cm)
Xét ΔABC có ED//AB
nên ED/AB=CD/CB
=>ED/21=20/35=4/7
=>ED=12(cm)
a: BC=căn 12^2+16^2=20cm
Xét ΔABC có AD là phân giác
nên BD/DC=AB/AC=3/4
=>BD/3=DC/4=(BD+DC)/(3+4)=20/7
=>BD=60/7cm; DC=80/7cm
Xét ΔCAB có ED//AB
nên ED/AB=CD/CB=4/7
=>ED/12=4/7
=>ED=48/7cm
b: S ABC=1/2*12*16=96cm2
BD/BC=3/7
=>S ABD/S ABC=3/7
=>S ABD=288/7cm2
Bổ sung đề: AC=28cm
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+28^2=1225\)
hay BC=35(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{DB}{21}=\dfrac{DC}{28}\)
mà DB+DC=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{21}=\dfrac{DC}{28}=\dfrac{DB+DC}{21+28}=\dfrac{35}{49}=\dfrac{5}{7}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{BD}{21}=\dfrac{5}{7}\\\dfrac{CD}{28}=\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=15\left(cm\right)\\CD=20\left(cm\right)\end{matrix}\right.\)
Xét ΔABC có
D∈BC(gt)
E∈AC(gt)
DE//AB(gt)
Do đó: \(\dfrac{DE}{AB}=\dfrac{CD}{CB}\)(Hệ quả Định lí Ta lét)
\(\Leftrightarrow\dfrac{DE}{21}=\dfrac{20}{35}\)
hay \(DE=\dfrac{21\cdot20}{35}=\dfrac{420}{35}=12\left(cm\right)\)
Vậy: CD=15cm; BD=20cm; DE=12cm
a) Xét \(\Delta ABC\) vuông tại A:
\(BC^2=AB^2+AC^2\) (Pytago).
Thay: \(BC^2=3^2+4^2.\)
\(\Rightarrow BC=5\left(cm\right).\)
Xét \(\Delta ABC:\)
BD là đường phân giác (gt).
\(\Rightarrow\dfrac{AD}{CD}=\dfrac{AB}{BC}\) (Tính chất đường phân giác).
\(\Rightarrow\dfrac{AD}{CD+AD}=\dfrac{AB}{BC+AB}.\)
\(\Rightarrow\dfrac{AD}{AC}=\dfrac{AB}{BC+AB}.\)
Thay: \(\dfrac{AD}{4}=\dfrac{3}{5+3}.\)
\(\Rightarrow AD=1,5\left(cm\right).\)
\(\Rightarrow CD=BC-AD=5-1,5=3,5\left(cm\right).\)
b) Xét \(\Delta ABC:\)
DK // AB (gt).
\(\Rightarrow\dfrac{BK}{CK}=\dfrac{AD}{CD}\left(Talet\right).\)
Mà \(\dfrac{AD}{CD}=\dfrac{AB}{BC}\left(cmt\right).\)
\(\Rightarrow\dfrac{BK}{CK}=\dfrac{AB}{BC}.\\ \Rightarrow BK.BC=AB.CK.\)
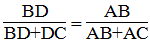
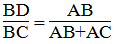
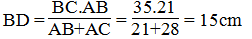
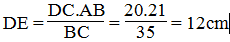
tôi ko biết làm
thế thì đừng tl