Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Áp dụng các hệ thức lượng trong tam giác vuông ABD, tính được BD = 25cm, OB = 9cm, OD = 16cm
b, Áp dụng các hệ thức lượng trong tam giác vuông DAC tính được OA = 12cm, AC = 100 3 cm
c, Tính được S = 1250 3 c m 2

a. tính dễ
b. tam giác ABO đồng dạng tam giác CDO => OB/OD = OA/OC
Tính được OA,OB,OD => OC => tính được AC
c. Sabcd = S tam giác ABD + S tam giác BDC

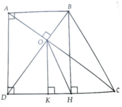
a, Tính được DB=15cm. A D B ^ ≈ 37 0 ; A B D ^ ≈ 53 0
b, Tính được AO=7,2cm, DO=9,6cm và AC=20cm
c, Kẻ OK ⊥ DC tại K
DH=AB=9cm, DC=16cm, DK=5,76cm và OK=7,68cm
Từ đó S D O H = O K . D H 2 = 7 , 68 . 9 2 = 34,56 c m 2

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AB^2=5^2-3^2=16\)
hay AB=4(cm)
Vậy: AB=4cm
b) Xét ΔCDE và ΔCAB có
\(\dfrac{CD}{CA}=\dfrac{CE}{CB}\left(\dfrac{1.5}{3}=\dfrac{2.5}{5}\right)\)
\(\widehat{ECD}=\widehat{ACB}\)(hai góc đối đỉnh)
Do đó: ΔCDE\(\sim\)ΔCAB(c-g-c)
Suy ra: \(\widehat{CDE}=\widehat{CAB}\)(hai góc tương ứng)
mà \(\widehat{CAB}=90^0\)(gt)
nên \(\widehat{CDE}=90^0\)
hay ED\(\perp\)BC
Ta có: ΔCDE\(\sim\)ΔCAB(cmt)
nên \(\dfrac{DE}{AB}=\dfrac{CD}{CA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{DE}{4}=\dfrac{1}{2}\)
hay DE=2(cm)
Vậy: DE=2cm

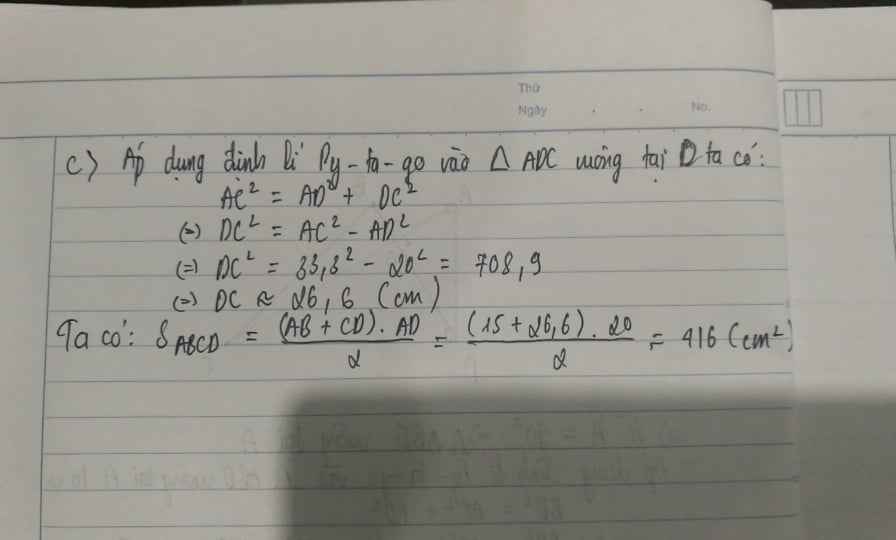
1 , áp dụng pii ta go vào tam giác vuông ABH suy ra AB = 15 cm
áp dụng hệ thức lượng ta có \(AB^2=BH.BC\)hay 15^2 =9 .BC => BC =25 cm
vậy s abc =\(\frac{1}{2}.12.25\)=150 \(cm^2\)
áp dụng pitago vào tam giác vuông ABD suy ra BD= 25 cm
áp dụng hệ thức lg tính ra đc BO = 9 cm
od 25 -9 =16 cm TA PHẢI TÍNH THÊM ao =căn (9.16)=12 cm
áp dụng hệ thức lg và tam giác vg acd suy ra AC= AD BÌNH / A0 =400/12 \(\approx\)33,3cm