Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Xét Δ ABM và Δ ECM có:
AM=ME (gt)
^AMB=^EMC( 2 góc đối đỉnh)
^A1=^E1(2 góc T/ứ)

a, Xét △ABC và △DCE có
AC = CD
C^ đối đỉnh
BC = CE
=> △ABC = △DCE
b, VÌ △ABC = △DCE nên góc BAC = góc CDE
=> CDE = 90 độ
c, Vì BE = BC + CE = 20
Mà BC = CE = \(\dfrac{BC}{2}\) = \(\dfrac{20}{2}\) = 10
Vì AD = AC + CD = 16
Mà AC = CD = \(\dfrac{AD}{2}\) = \(\dfrac{16}{2}\) = 8
Áp dụng định lý Pytago
ta có : \(BC^2=AB^2+AC^2\)
\(10^2=AB^2+8^2\)
\(100=AB^2+64\)
\(AB^2=100-64=36\)
Vậy \(AB=6^2\)
Mong bạn tick cho mik :))

b: Xét ΔMND và ΔMPD có
MN=MP
ND=PD
MD chung
Do đó: ΔMND=ΔMPD

a: Xét ΔACI và ΔMCI có
CA=CM
ˆACI=ˆMCIACI^=MCI^
Do đó: ΔACI=ΔMC

vì dùng máy tính nên ko vẽ hình đc thông cảm !!
a) giả thiết
Δ ABC cân tại A
AK là tia đối của AB
BK=BC
KH⊥BC(H∈BC)
KH cắt AC tại E
Kết luận
KH=AC
BE là tia phân giác của góc ABC
b) xét tam giác BAC và tam giác BHK có
\(\widehat{B} \) Chung
KH=BC (gt)
\(\widehat{BAC}=\widehat{BHK}=90\) (gt)
tam giác BAC = tam giác BHK (ch-gn)
=>KH=AC(2 góc tương ứng )
b)Xét Δ KBC có BK=BC(gt)
=> tam giác KBC cân tại B
Mà KH⊥BC=> KH là đường cao
AC⊥AB =>AC⊥KB(K∈AB)=>AC là đường cao
Mà AC giao vs KH tại E
=> E là trực tâm của tam giác
=> BE là đường cao (tc 3 đg cao trong tam giác)
=> BE là giân giác của góc \(\widehat{KBC}\)
=>BE là giân giác của góc \(\widehat{ABC} \) (A∈BK)

a: AB=30cm
b: Xét ΔMCA và ΔMBE có
MC=MB
\(\widehat{AMC}=\widehat{EMB}\)
MA=ME
Do đó:ΔMCA=ΔMBE
Suy ra: \(\widehat{MCA}=\widehat{MBE}=90^0\)
hay ΔMBE vuông tại B

a:
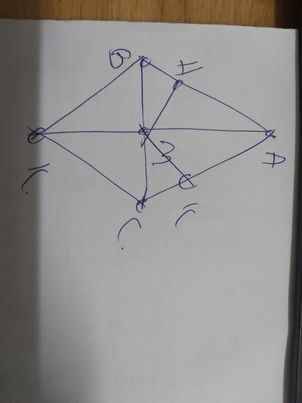
| GT | ΔABC cân tại A M là trung điểm của BC MK=MA MH\(\perp\)AB; MK\(\perp\)AC H\(\in\)AB; K\(\in\)AC |
| KL | b: ΔABM=ΔACM c: ΔABM=ΔKCM d: AB//CK e: MH=MK |
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
c: Xét ΔMAB và ΔMKC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMKC
d: Ta có: ΔMAB=ΔMKC
=>\(\widehat{MAB}=\widehat{MKC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//KC
e: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>MH=MK
=>ΔMHK cân tại M

b: \(\widehat{C}=60^0\)
c: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
d: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: AB//CD
e: Ta có: ΔCBA vuông tại A
mà AM là đường trung tuyến
nên AM=BC/2
hay BC=2AM