Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, HS tự chứng minh
b, Ta chứng minh được B E ⏜ = C D ⏜ từ đó suy ra BE = CD và tứ giác BDEC là hình thang cân

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)
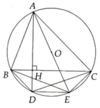
A B C D E H O M
a) Từ O kẻ OM vuông góc với AD
Khi đó theo tính chất của đường kính và dây cung thì M là trung điểm AD
Lại có O là trung điểm AE => MO là đường trung bình của tam giác ADE
=> MO // DE , lại có MO // BC (cùng vuông góc với AD)
=> DE // BC
b) Tứ giác ABDC nột tiếp đường tròn (O)
=> \(\widehat{ADB}=\widehat{BCA}\Leftrightarrow90^0-\widehat{ADB}=90^0-\widehat{BCA}\Rightarrow\widehat{CBD}=\widehat{ECB}\)
Lại có từ phần a, BED là hình thang vì có BC // DE
=> BCED là hình thang cân
a, Xét ΔADE nội tiếp đường tròn đường kính AE
=> AD ⊥ DE (1)
LẠi có AH ⊥ BC = > AD ⊥ BC (2)
Từ (1) và (2) => DE // BC ( cùng vuông góc với AD) (*)
b, Ta có: Tứ giác ABDC nội tiếp
=> ˆADBADB^= ˆACBACB^
Lại có : ˆCBDCBD^ + ˆADBADB^ = ˆACBACB^ + ˆECBECB^ ( cùng bằng 90 độ)
=> ˆCBDCBD^ = ˆECBECB^ (**)
Từ (*) và (**) => BCED là hình thang cân