Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

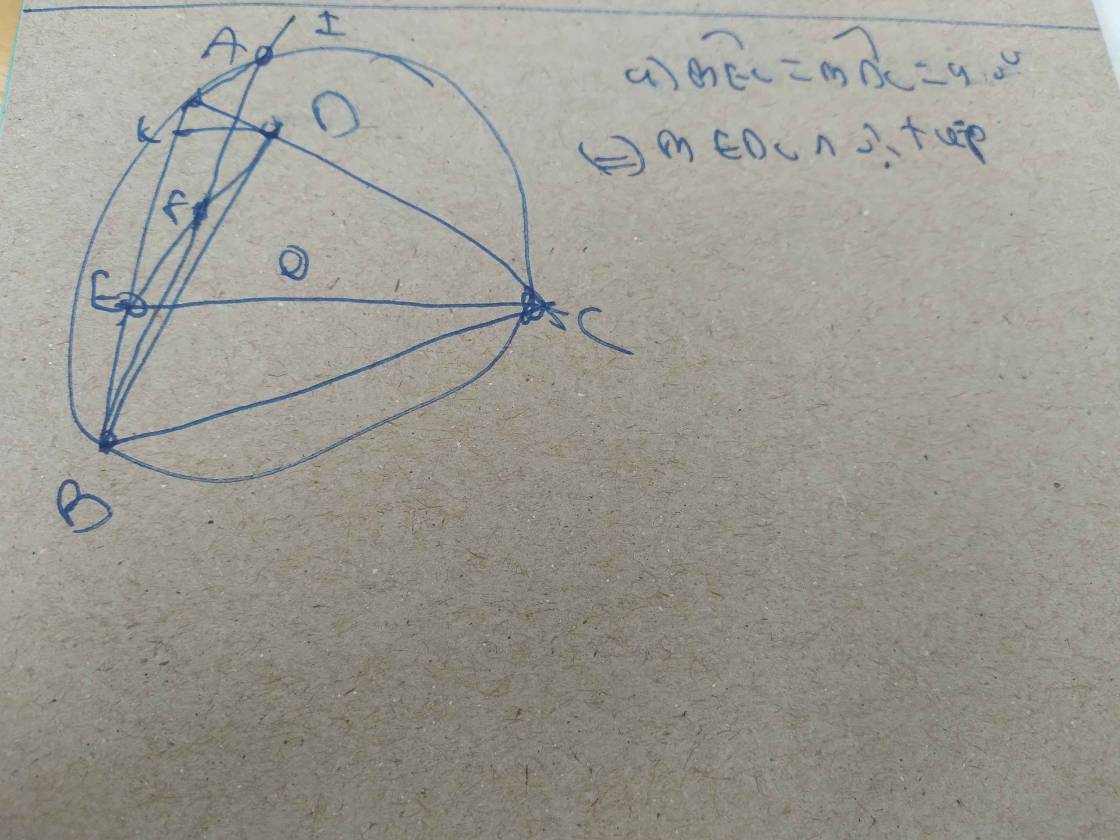
A B C D E F H P K I G M O
c) Gọi K là giao điểm của EF và AH, I và G lần lượt là trung điểm của EF và AH.
Ta thấy \(\left(DKHA\right)=-1\),G là trung điểm của HA => \(DK.DG=DH.DA=DB.DC\)
=> K là trực tâm của \(\Delta\)BGC => CK vuông góc BG
Vì CK vuông góc BG, BH vuông góc AC nên \(\widehat{ACK}=\widehat{HBG}\)(1)
Ta có \(\widehat{AEF}=\widehat{ABC}=\widehat{APC}\)=> (P,K,E,C)cyc => \(\widehat{ACK}=\widehat{APM}=\widehat{ABM}\)(2)
Lại có \(\Delta\)BFE ~ \(\Delta\)BHA, I và G lần lượt là trung điểm của FE và HA => \(\widehat{HBG}=\widehat{FBI}\)(3)
Từ (1);(2);(3) suy ra \(\widehat{ABM}=\widehat{FBI}\), mà BF trùng BA nên B,I,M thẳng hàng hay BM chia đôi EF.
Bạn tham khảo thêm cách này:
Ta có \(\widehat{FGE}+\widehat{FDE}=2\widehat{BAC}+(180^0-2\widehat{BAC})=180^0\)
=> Tứ giác FGED nội tiếp, vì DG là phân giác góc EDF nên \(\Delta\)DFK ~ \(\Delta\)DGE (g.g)
=> \(DK.DG=DE.DF\)
Lại có \(\Delta\)DBF ~ \(\Delta\)DEC (g.g) => \(DE.DF=DB.DC\)
Suy ra \(DK.DG=DB.DC\)=> \(\Delta\)BDK ~ \(\Delta\)GDC (c.g.c)
=> \(\widehat{DBK}=\widehat{DGC}\). Mà \(\widehat{DGC}\)phụ \(\widehat{GCB}\)nên BK vuông góc GC
Vậy K là trực tâm tam giác BGC.

AH cắt đường tròn tâm O tại M . Tam giác abd có dk là đường cao nên bk.ba=bd.bd mà bk.ba = bf.bi nên bd.bd =bf.bi
Nên bf/bd=bd/bi và góc ibd chung
Nên tam giác bfd đồng dạng tam giác bdi
Nên góc bdi = góc bid mà bdi=ecb=bcm
mà góc bia= góc bca
Cộng lại được aid=dcm
Aicm nội tiếp nên aim = dcm . Từ đó suy ra aid=aim
Nên i,d,m thẳng hàng nên ah và id cắt nhau tại điểm thuộc đường trón tâm o

a: Xéttứ giác AEHF có góc AEH+góc AFH=180 độ
nên AEHF là tứ giác nội tiếp
c: Xét tứ giác AEDC có góc ADC=góc AEC=90 độ
nên AEDC là tứ giác nội tiếp
d: góc EDA=góc ABF
góc FDA=góc FDH=góc ACE
mà góc ABF=góc ACE
nên góc EDA=góc FDA
=>DA là phân giác của góc EDF

a) Xét tứ giác BFHD có
\(\widehat{BFH}\) và \(\widehat{BDH}\) là hai góc đối
\(\widehat{BFH}+\widehat{BDH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BFHD là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BFC}\) và \(\widehat{BEC}\) cùng nhìn cạnh BC một góc bằng 900
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

a: góc OBE+góc OCE=180 độ
=>OBEC nội tiếp
b: Xét ΔEBD và ΔEAB có
góc EBD=góc EAB
góc BED chung
=>ΔEBD đồng dạng với ΔEAB
=>EB/EA=ED/EB
=>EB^2=EA*ED