Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Xét tg DHB và tg DCA có: ^HDB=^CDA=90 độ, ^DBH=^DAC ( cùng phụ với hai góc bằng nhau BHD=^AHE)
Do đó: tg HDB đồng dạng tg DCA (g.g)
Suy ra: HD/DC=BD/DA-> bd*dc=dh*da
b, HD/HA=SBHC/SABC
HE/BE=SAHC/SABC
HF/CF=SHAB/SABC
HD/HA+HE/BE+HF/CF=SBHC/SABC+SAHC/SABC+SAHB/SABC=1

Hơi khó nên tui dung tạm BĐT vậy , bạn thông cảm ^ ^
A B C H E F H
\(S\left(ABC\right)=AD.\frac{BC}{2}\)
\(S\left(BHC\right)=HD.\frac{BC}{2}\)
\(\Rightarrow\frac{HD}{AD}=\frac{S\left(BHC\right)}{S\left(ABC\right)}\left(1\right)\)
Tương tự:
\(\frac{HE}{BE}=\frac{S\left(AHC\right)}{S\left(ABC\right)}\left(2\right)\)
\(\frac{HF}{CF}=\frac{S\left(AHB\right)}{S\left(ABC\right)}\left(3\right)\)
(1) + (2) +(3) được:
\(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=\left[S\left(BHC\right)+S\left(AHC\right)+\frac{S\left(AHB\right)}{S\left(ABC\right)}\right]=\frac{S\left(ABC\right)}{S\left(ABC\right)}=1\)
Áp dụng bất đẳng thức: \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)9 ta có:
\(\left(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}\right)\left(\frac{AD}{HD}+\frac{BE}{HE}+\frac{CF}{HF}\right)\ge9\)
mà: \(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=1\) \(\Rightarrow\left(\frac{AD}{HD}+\frac{BE}{HE}+\frac{CF}{HF}\right)\ge9\)

Ad ĐỪNG XÓA
Học tiếng anh free vừa học vừa chơi đây
các bạn vào đây đăng kí nhá : https://iostudy.net/ref/165698

< Bạn tự vẽ hình nha>
a)Xét ΔABE và ΔACF, ta có:
góc A: chung
góc F=góc E= 90o
Vậy ΔABE ∼ ΔACF (g.g)
b)Xét ΔHEC và ΔHFB là:
góc H: chung
H1=H2(đối đỉnh)
Vậy ΔHEC∼ ΔHFB (g.g)
⇒\(\dfrac{HE}{HF}\)=\(\dfrac{HC}{HB}\)⇔HE.HB=HF.HC
<Mình chỉ biết đến đó thôi>![]()

a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔAEB∼ΔAFC(g-g)
b) Ta có: ΔAEB∼ΔAFC(cmt)
nên \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)(cmt)
\(\widehat{BAC}\) chung
Do đó: ΔAEF∼ΔABC(c-g-c)
 đó nha bn
đó nha bn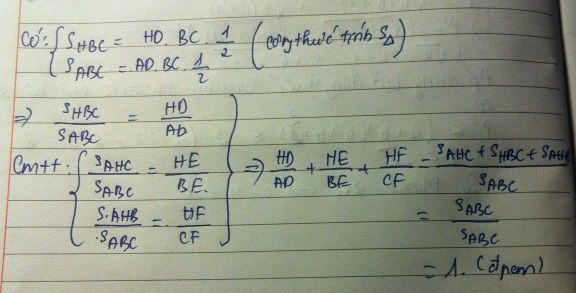
Em tự vẽ hình nhé.
Ta có: \(\frac{AD}{HD}=\frac{S_{ABC}}{S_{BHC}};\frac{BE}{HE}=\frac{S_{ABC}}{S_{AHC}};\frac{CF}{FH}=\frac{S_{ABC}}{S_{AHB}}\)
Đặt \(S_{ABC}=1;S_{BHC}=a;S_{ACH}=b;S_{AHB}=c.\)
Khi đó ta có: \(a+b+c=1;\frac{AD}{HD}+\frac{BE}{HE}+\frac{CF}{HF}=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
Áp dụng bất đẳng thức Cosi cho 3 số dương, ta có:
\(a+b+c\ge3\sqrt[3]{abc};\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}\)
Vậy thì \(\Rightarrow\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\) mà a + b + c = 1 nên \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge9\Rightarrow\frac{AD}{HD}+\frac{BE}{HE}+\frac{CF}{HF}\ge9\)
cam on nha