Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=180^0\)
nên AEHF là tứ giác nội tiếp
b: Xét ΔABE vuông tại E và ΔHCE vuông tại E có
\(\widehat{ABE}=\widehat{HCE}\)
Do đó: ΔABE\(\sim\)ΔHCE
Suy ra: AB/HC=BE/CE
hay \(AB\cdot CE=BE\cdot HC\)
a) Xét tứ giác AEHF có
\(\widehat{AFH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{AFH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BFC}\) và \(\widehat{BEC}\) là hai góc cùng nhìn cạnh BC
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: BFEC nội tiếp
=>góc HFE=góc HBC
=>góc HFE=góc HNM
=>FE//MN
a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
nên AEHF là tứ giác nội tiếp
b: Xét ΔFAC vuông tại F và ΔFHB vuông tại F có
\(\widehat{FCA}=\widehat{FBH}\left(=90^0-\widehat{BAE}\right)\)
Do đó: ΔFAC đồng dạng với ΔFHB
=>\(\dfrac{FA}{FH}=\dfrac{FC}{FB}\)
=>\(FA\cdot FB=FC\cdot FH\)
c: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>\(\widehat{FEC}+\widehat{FBC}=180^0\)
mà \(\widehat{FEC}+\widehat{AEF}=180^0\)(hai góc kề bù)
nên \(\widehat{AEF}=\widehat{ABC}\)(1)
Kẻ tiếp tuyến Ax của (O)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{xAC}=\widehat{AEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ax//FE
Ta có: Ax//FE
OA\(\perp\)Ax
Do đó: OA\(\perp\)EF
a: góc AFH+góc AEH=180 độ
=>AEHF nội tiếp
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
b: BFEC nội tiếp
=>góc IBF=góc IEC
Xét ΔIBF và ΔIEC có
góc IBF=góc IEC
góc I chung
=>ΔIBF đồng dạng với ΔIEC
=>IB/IE=IF/IC
=>IB*IC=IE*IF
Câu 8:
a) Xét tứ giác BFEC có
\(\widehat{BFC}\) và \(\widehat{BEC}\) là hai góc cùng nhìn cạnh BC
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
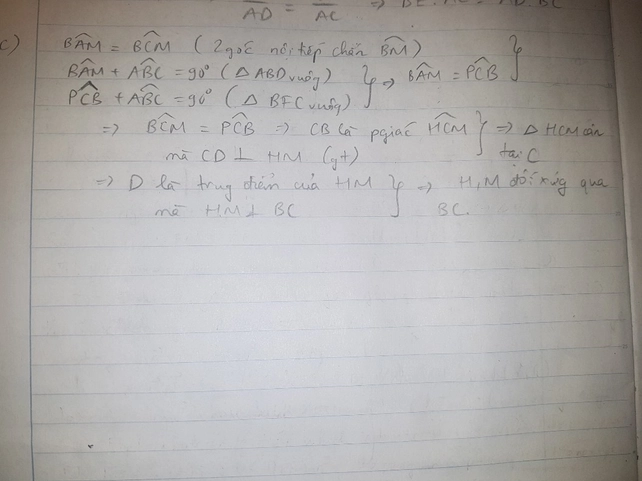Bạn tham khảo nhé!
c: Vì góc B là góc nội tiếp chắn cung nhỏ AC
nên \(sđ\stackrel\frown{AC}=2\cdot\widehat{B}=120^0\)
Lời giải:
Vì $AD, BE, CF$ là đường cao của tam giác $ABC$ và cắt nhau tại $H$ nên $\widehat{HFA}=\widehat{HEA}=90^0$
Tứ giác $AEHF$ có tổng hai góc đối nhau $\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0$ nên $AEHF$ là tứ giác nội tiếp.
------------------
Kẻ tiếp tuyến $Ax$ của $(O)$. Ta có $OA\perp Ax(1)$
$\widehat{xAB}=\widehat{ACB}=\widehat{ECB}(2)$ (góc tạo bởi tiếp tuyến và dây cung bằng góc nt chắn cung đó - cung $AB$)
Tứ giác $BFEC$ có $\widehat{BFC}=\widehat{BEC}=90^0$ và cùng nhìn cạnh $BC$ nên $BFEC$ là tứ giác nội tiếp.
$\Rightarrow \widehat{ECB}=\widehat{AFE}(3)$
Từ $(2); (3)\Rightarrow \widehat{xAB}=\widehat{AFE}$
Mà 2 góc này ở vị trí so le trong nên $Ax\parallel EF(4)$
Từ $(1); (4)\Rightarrow OA\perp EF$
Hình vẽ: