
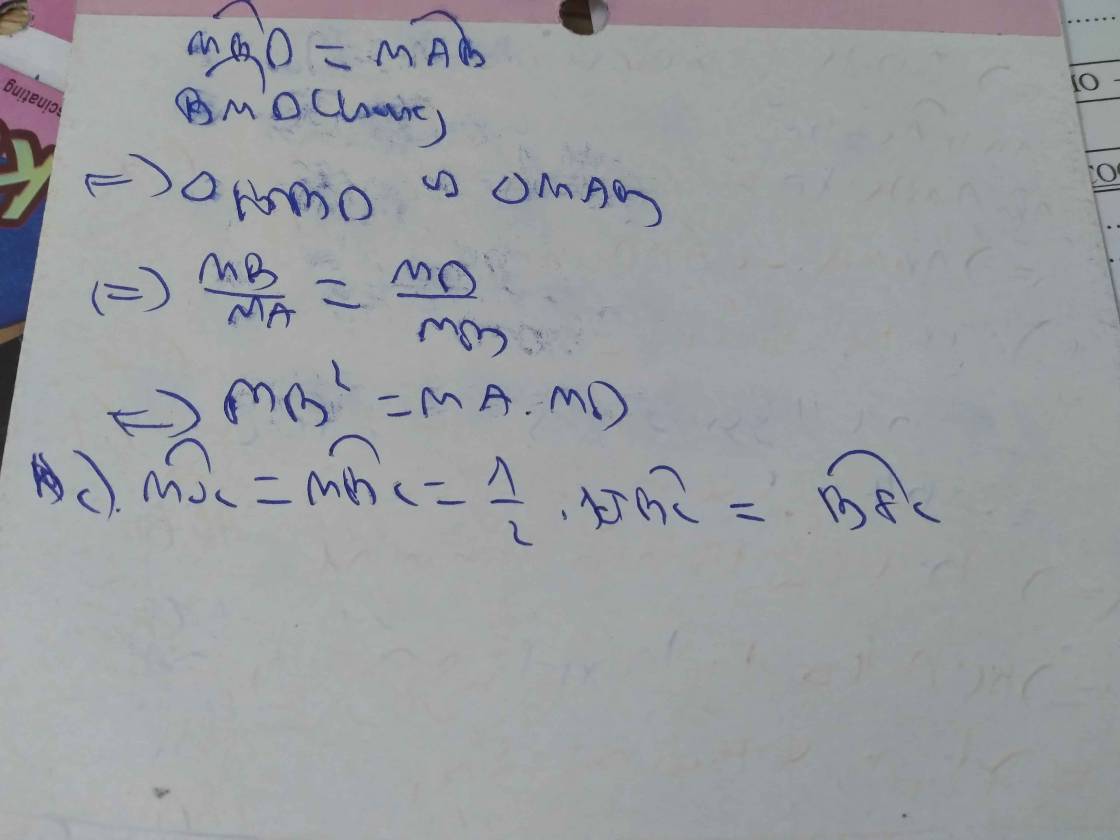
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


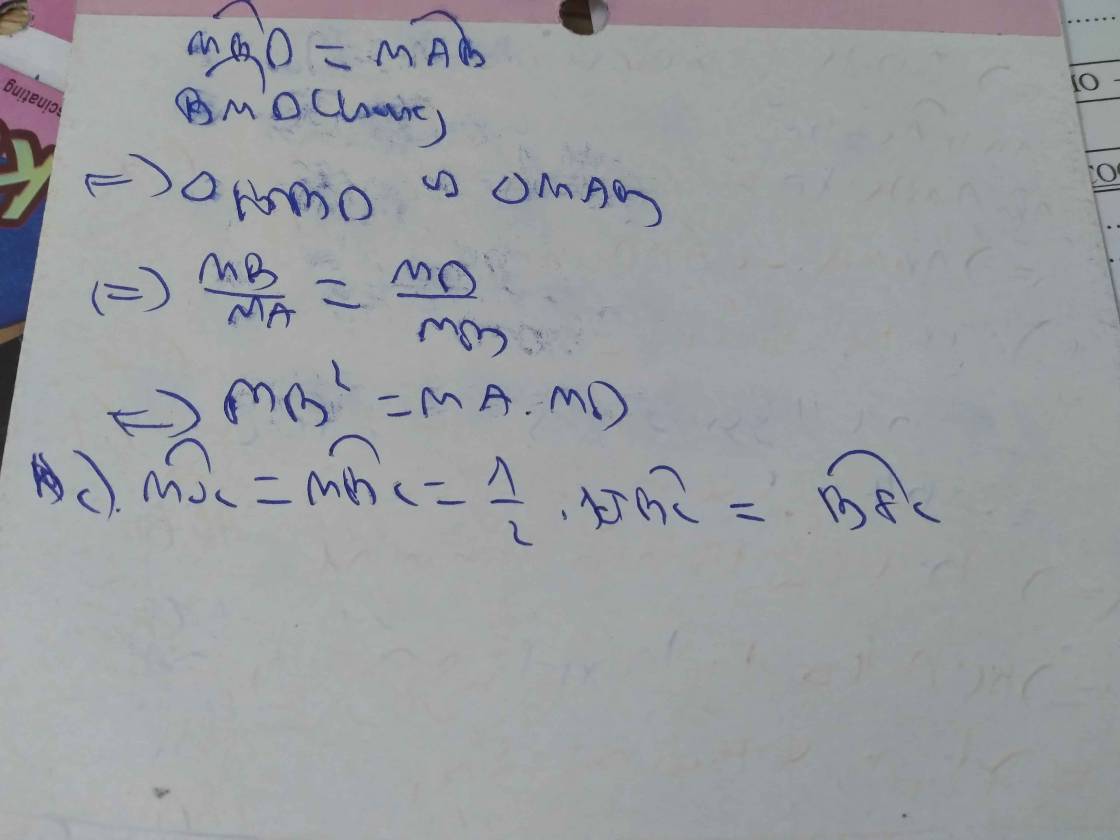

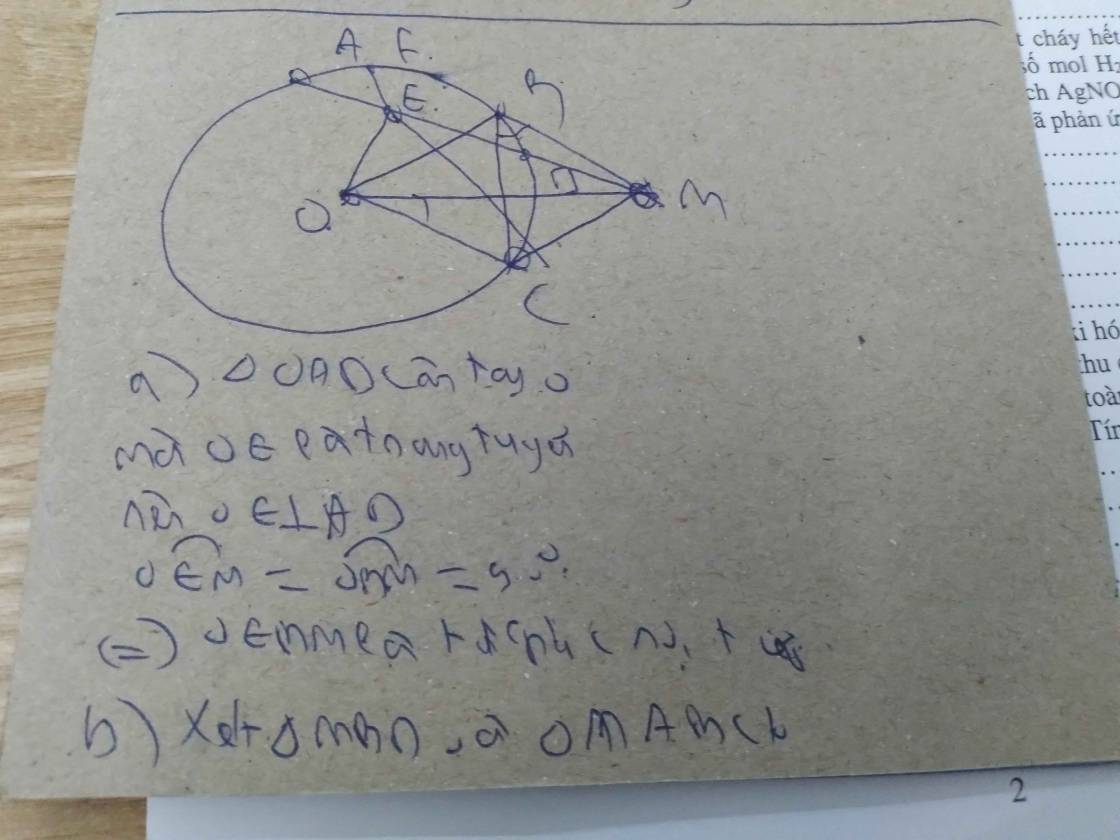
a, O B M ^ = O E M ^ = 90 0
=> Tứ giác OEBM nội tiếp
b, Chứng minh được: ∆ABM:∆BDM (g.g) => M B 2 = M A . M B
c, DOBC cân tại O có OM vừa là trung trực vừa là phân giác
=> M O C ^ = 1 2 B O C ^ = 1 2 s đ B C ⏜
Mà B F C ^ = 1 2 B C ⏜ => M O C ^ = B F C ^
d, O E M ^ = O C M ^ = 90 0 => Tứ giác EOCM nội tiếp
=> M E C ^ = M O C ^ = B F C ^ mà 2 góc ở vị trí đồng vị => FB//AM

a,Xét đường tròn (O) có:
MB là tiếp tuyến của đường tròn (gt) => \(\widehat{OBM}=90^0\)
Mặt khác E là trung điểm của AD (gt) => \(OE\perp AD\) => \(\widehat{OEM}=90^0\) => \(\widehat{OBM}=\widehat{OEM}\)
Xét tứ giác OEBM có: \(\widehat{OBM}=\widehat{OEM}\) (cmt)
=> OEBM là tứ giác nội tiếp
b, Xét đường tròn (O), tiếp tuyến MB, dây cung BD có:
\(\widehat{MBD}\) là góc tạo bởi tiếp tuyến và dây cung và \(\widehat{MAB}\) là góc nội tiếp cùng chắn cung BD => \(\widehat{MBD}=\widehat{MAB}\)
Xét \(\Delta MBD\) và \(\Delta MAB\) có:
\(\widehat{MBD}=\widehat{MAB}\) (cmt)
\(\widehat{M}\) là góc chung
=> \(\Delta MBD\) ~ \(\Delta MAB\left(g.g\right)\)
=> \(\dfrac{MB}{MA}=\dfrac{MD}{MB}\) => \(MB^2=MA.MD\)
c, Gọi giao điểm của OM với (O) là I
Xét đường tròn (O), tiếp tuyến MA, MB có: MA cắt MB tại M
=> \(\widehat{IOB}=\widehat{IOC}=\dfrac{1}{2}\widehat{BOC}\) (t/c của 2 tiếp tuyến cắt nhau)
=> cung IB = cung IC
Mặt khác \(\widehat{BOC}\) là góc ở tâm và \(\widehat{BAC}\) là góc nội tiếp cùng chắn cung BC => \(\widehat{BAC}=\dfrac{1}{2}\widehat{BOC}\)
=> \(\widehat{BAC}=\widehat{IOC}\). Hay \(\widehat{BAC}=\widehat{MOC}\)
Ta có: \(\widehat{BAC}\) và \(\widehat{BFC}\) là các góc nội tiếp cùng chắn cung BC
=> \(\widehat{BAC}=\widehat{BFC}\)
=> \(\widehat{BFC}=\widehat{MOC}\)
d, Gọi giao điểm của OE và DF là K
Ta có: \(\widehat{OEM}=90^0\left(cmt\right)\) => \(KE\perp AD\)
Xét \(\Delta AKD\) có:
E là trung điểm của KD (gt)
\(KE\perp AD\left(gt\right)\)
=> \(\Delta AKD\) cân tại K => \(\widehat{KAD}=\widehat{KDA}\). Hay \(\widehat{BAD}=\widehat{FDA}\)
Xét đường tròn (O) có: \(\widehat{BAD}\) và \(\widehat{BFD}\) là các góc nội tiếp cùng chắn cung BD => \(\widehat{BAD}=\widehat{BFD}\)
=> \(\widehat{BFD}=\widehat{FDA}\)
Mà 2 góc này ở vị trí so le trong => BF // AD. Hay BF // AM

Do BM là tiếp tuyến của đường tròn nên \widehat{OBM}=90^o
o
Xét đường tròn (O) có AD là một dây cung. Lại có E là trung điểm AD nên theo tính chất của đường kính và dây cung, ta có OE\perp ADOE⊥AD hay \widehat{OEM}=90^oOEM=90o.
Xét tứ giác OEBM có \widehat{OBM}=\widehat{OEM}=90^oOBM=OEM=90o, chúng lại là hai góc kề nhau nên OEBM là tứ giác nội tiếp.
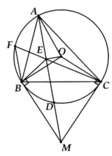
Cho tam giác ABCABC có ba góc nhọn nội tiếp đường tròn tâm OO (AB < AC)(AB<AC). Hai tiếp tuyến tại BB và CC cắt nhau tại MM. AMAM cắt đường tròn (O)(O) tại điểm thứ hai DD. Gọi EE là trung điểm đoạn ADAD. Chứng minh OEBMOEBM là tứ giác nội tiếp.

theo bai ta co E là trung điểm đoạn ADAD
ma AD la mot day cung thuoc (O)
=> OE vuong goc voi AD
hay goc OEM = 90 (1)
Mat khac, BM vuong goc voi OB tai B (gt)
hay goc OBM= 90 (2)
Tu (1) va (2) suy ra tu giac OEBM noi tiep

\(\Delta\)EAC đông dạng EBD
=> k = EA / EB = AC / BD = R/2 / ( 2R+R/2) = 1/5