Cho tam giác MNP vuông tại M (MN<MP) đường cao MH. a) Chứng minh : ΔHNM ~ ΔMNP b) Chứng minh : MH

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

NC

Nguyễn Chi

26 tháng 3 2019

Cho tam giác MNP vuông tại M (MN<MP) đường cao MH.

a) Chứng minh : ΔHNM ~ ΔMNP

b) Chứng minh : MH² = HN.HP

c) Trên tia đối của tia MN lấy điểm K sao cho MK = MN. Gọi I là trung điểm của MH. Chứng minh: HK.MP = NK.IP

#Hỏi cộng đồng OLM #Toán lớp 8

1

LT

Lê Thu Dương

26 tháng 3 2019

https://i.imgur.com/JJdFoD1.jpg

Các câu hỏi dưới đây có thể giống với câu hỏi trên

NT

Ninh Thanh Tú Anh

19 tháng 6 2020 - olm

cho tam giác mnp vuông tại m đường cao mh, trên tia đối của mp lấy a sao cho an vuông np. i trung điểm mh, pi cắt na tại a. k là giao điểm oi và nm.

chứng minh a, k, h thằng hàng

#Hỏi cộng đồng OLM #Toán lớp 8

0

ND

Nguyễn Đức An

19 tháng 6 2021 - olm

Cho tam giác MNP vuông tại M. MH là đường cao (H thuộc NP) 1) Chứng minh tam giác HNM đồng dạng tam giác MNP 2) Cho MN = 9cm, MP = 12cm a) Tính độ dài đoạn thẳng NH b)Gọi I là trung điểm của MN, kẻ HK vuông góc với MP tại K. Gọi E là giao điểm của KH và IP. Chứng minh E là trung điểm của HK và tính diện tích tứ giác MKEI 3) Chứng minh MH, PI, NK đồng quy

#Hỏi cộng đồng OLM #Toán lớp 8

0

NT

Nguyễn Tiến Mạnh

8 tháng 11 2023

Cho tam giác MNP vuông tại M có đường cao MH; kẻ HD vuông góc với MN (D ∈ MN), HE vuông góc với MP (E ∈ MP)

a) Chứng minh tứ giác MEDH là hình chứ nhật

b) Gọi O là trung điểm của MH, chứng minh DO=OE

c) Gọi I, K lần lượt là trung điểm của NH và HP, chứng minh DI//EK

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

8 tháng 11 2023

a: Xét tứ giác MDHE có

\(\widehat{MDH}=\widehat{MEH}=\widehat{EMD}=90^0\)

=>MDHE là hình chữ nhật

b: MDHE là hình chữ nhật

=>MH cắt DE tại trung điểm của mỗi đường

mà O là trung điểm của MH

nên O là trung điểm của DE

=>DO=OE

c: ΔHDN vuông tại D

mà DI là đường trung tuyến

nên DI=HI=IN

=>ΔIHD cân tại I

ΔPEH vuông tại E

mà EK là đường trung tuyến

nên EK=KP=KH

=>ΔKEH cân tại K

\(\widehat{KED}=\widehat{KEH}+\widehat{DEH}\)

\(=\widehat{KHE}+\widehat{HMD}\)

\(=\widehat{HMD}+\widehat{HND}=90^0\)

=>KE vuông góc ED(1)

\(\widehat{IDE}=\widehat{IDH}+\widehat{EDH}\)

\(=\widehat{IHD}+\widehat{EMH}\)

\(=\widehat{HPM}+\widehat{HMP}=90^0\)

=>ID vuông góc DE(2)

Từ (1) và (2) suy ra DI//EK

NT

Nguyễn Tiến Mạnh

8 tháng 11 2023

cảm ơn nha bạn

HH

Hoàn Hà

4 tháng 5 2023

Cho tam giác MNP vuông tại M, đường cao MH a) chứng minh tam giác HNM đồng dạng tam giác MNP b) chứng minh hệ thức MH²= NH.PH c) Lấy điểm E tùy ý trên cạnh MP ( E khác M,P) .vẽ điểm F trên cạnh MN sao cho góc FHE = 90°. Chứng minh tam giác NFH đồng dạng tam giác MEH và góc NMH = góc FEH. d) xác định vị trí của điểm E trên MP sao cho diện tích tam giác HÈ đạt giá trị nhỏ nhất

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

10 tháng 5 2023

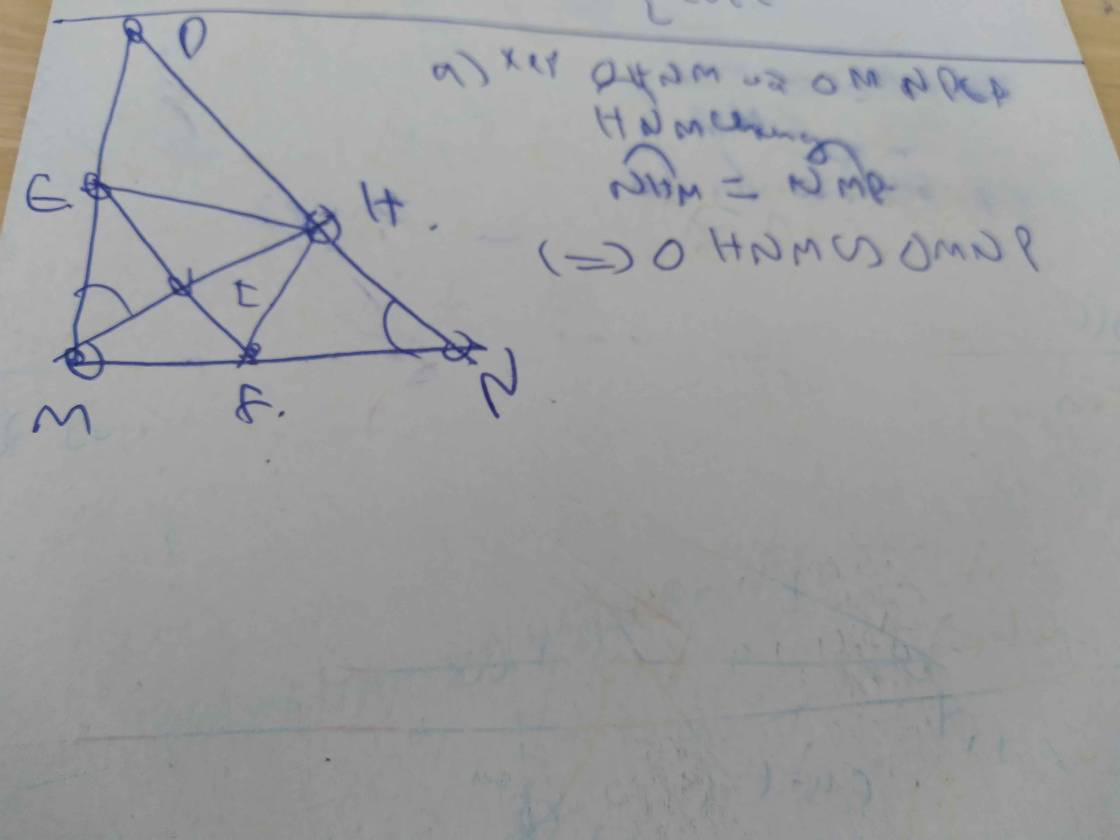
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có

góc N chung

=>ΔHNM đồng dạng với ΔMNP

b: ΔMNP vuông tại M co MH vuông góc NP

nên MH^2=HN*HP

AN

an ngô

21 tháng 4 2023

Cho tam giác MNP vuông tại M, đường cao MH . a) Chứng minh DHNM đồng dạng với DMNP.b) Chứng minh hệ thức . Lấy điểm E tùy ý trên cạnh MP( E khác M; P) , vẽ điểm F trên cạnh MN sao cho , EF cắt MH tại điểm I. Chứng minh DNFH đồng dạng với DMEH và ...

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

22 tháng 4 2023

loading...

PK

phạm khánh linh

7 tháng 9 - olm

Cho tam giác ABC nhọn AB nhỏ hơn AC kẻ đường cao AD be CF cắt nhau tại H Gọi M là trung điểm bc Trên tia đối của MH lấy N sao cho MH = MN a tứ giác bhcn là hình gì B Chứng minh Bac + góc B NC = 180 độ. trên tia đối của tia DH lấy K sao cho dh = DK Chứng minh tứ giác bcn k là hình thang cân

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

7 tháng 9

a: Xét tứ giác BHCN có M là trung điểm chung của BC và HN

nên BHCN là hình bình hành

b: BHCN là hình bình hành

=>BH//CN

mà BH⊥AC

nên CN⊥CA

Ta có: BHCN là hình bình hành

=>CH//BN

mà CH⊥BA

nên BN⊥BA

Xét tứ giác ABNC có \(\hat{ABN}+\hat{ACN}+\hat{BAC}+\hat{BNC}=360^0\)

=>\(\hat{BAC}+\hat{BNC}=360^0-90^0-90^0=180^0\)

c: Xét ΔHKN có

D,M lần lượt là trung điểmcủa HK,HN

=>DM là đường trung bình của ΔHKN

=>DM//KN

=>BC//KN

Xét ΔCHK có

CD là đường cao

CD là đường trung tuyến

Do đó: ΔCHK cân tại C

=>CH=CK

mà CH=BN

nên CK=BN

Xét tứ giác BCNK có

BC//NK

BN=CK

Do đó: BCNK là hình thang cân

TT

thanh trúc

28 tháng 4 2022

Cho tam giác MNP vuông tại M vẽ đường cao MH, biết MN =3cm, MP = 4cm

a/ Chứng minh ∆HNM ~ ∆MNP

b/ Tính NP , MH , NH.

c/ Gọi I và K lần lượt hình chiếu của điểm H lên cạnh MN, MP.

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

20 tháng 6 2023

a: Xét ΔHNM vuông tại H và ΔMNP vuôg tại M có

góc N chung

=>ΔHNM đồng dạng với ΔMNP

b: NP=căn 3^2+4^2=5cm

MH=3*4/5=2,4cm

NH=3^2/5=1,8cm

c; Đề bài yêu cầu gì?

N

NARUTO3D

18 tháng 4 2019 - olm

cho tam giác MNP vuông tại M , đường cao MH.

a, chứng minh tam giác HNM đồng dạng tam giác MNP.

b, chứng minh MH^2=NH x PH.

c, lấy điểm E tùy trên cạnh MP, vẽ điểm F trên cạnh MN sao cho góc FHE=90 độ. chứng minh tam giác NFH đồng dạng tam giác MEH và góc NMH = FEH

>_< please, help me now!!!

#Hỏi cộng đồng OLM #Toán lớp 8

0

NQ

Nhi Quỳnh

6 tháng 5 2023

Cho ΔMNP vuông tại M có MN = 9cm, MP = 12cm. Vẽ MH vuông góc với NP tại H

a) Chứng minh ΔHNM và ΔMNP đồng dạng

b) Tính diện tích tam giác MHP

c) Vẽ tia phân giác MD của góc NMH (D ∈ NH). Chứng minh: ND.MP = DH.NP

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

10 tháng 5 2023

a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có

góc N chung

=>ΔHMN đồng dạng vói ΔMNP

b: \(NP=\sqrt{9^2+12^2}=15\left(cm\right)\)

MH=9*12/15=108/15=7,2cm

HP=12^2/15=9,6cm

S MHP=1/2*9,6*7,2=34,56cm²