Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{MN}{MP}=\dfrac{3}{4}\Rightarrow MN=\dfrac{3}{4}MP\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{MI^2}=\dfrac{1}{MN^2}+\dfrac{1}{MP^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{48}{5}\right)^2}=\dfrac{1}{\left(\dfrac{3}{4}MP\right)^2}+\dfrac{1}{MP^2}\)
\(\Rightarrow MP^2=\dfrac{20736}{625}\Rightarrow MP=\dfrac{144}{25}\)
\(\Rightarrow MN=\dfrac{3}{4}MP=\dfrac{108}{25}\)
\(NP=\sqrt{MN^2+MP^2}=\dfrac{36}{5}\)
b. Áp dụng hệ thức lượng:
\(MP^2=IP.NP\Rightarrow IP=\dfrac{MP^2}{NP}=\dfrac{576}{125}\)
\(S_{MIP}=\dfrac{1}{2}IP.MI=\dfrac{13824}{625}\)

a: ΔPIM vuông tại I
=>IP^2+IM^2=MP^2
=>IM^2=10^2-6^2=64
=>IM=8(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên PI*PN=PM^2
=>PN=10^2/6=50/3(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên MI^2=IN*IP
=>IN=8^2/6=32/3(cm)
Xét ΔMNP vuông tại M có sin MNP=MP/PN
=10:50/3=3/5
=>góc MNP=37 độ
b: C=MN+NP+MP
=10+40/3+50/3
=10+90/3
=10+30
=40(cm)
c: Xét ΔIMP vuông tại I có IK là đường cao
nên IK*PM=IP*IM
=>IK*10=6*8=48
=>IK=4,8(cm)

a: MN/MP=3/4 nên IN/IP=9/16
=>IN=9/16IP
Ta có: \(MI^2=IN\cdot IP\)
\(\Leftrightarrow IP^2\cdot\dfrac{9}{16}=9.6^2\)
=>IP=12,8(cm)
IN=9/16x12,8=7,2cm
NP=7,2+12.8=20cm
\(MN=\sqrt{7.2\cdot20}=12\left(cm\right)\)
MP=16cm
b: \(S_{MIP}=\dfrac{9.6\cdot12.8}{2}=9.6\cdot6.4=61.44\left(cm^2\right)\)
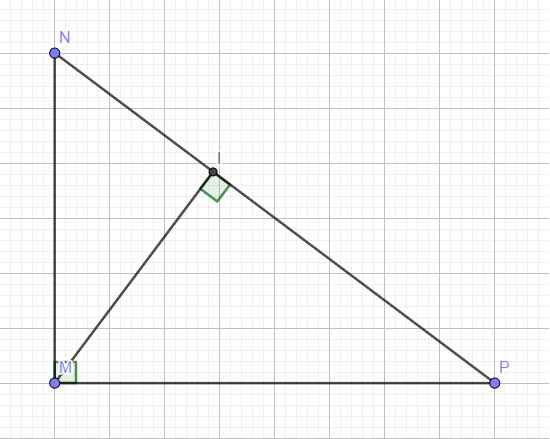

a: MN/MP=3/4 nên IN/IP=9/16
=>IN=9/16IP
Ta có: \(MI^2=IN\cdot IP\)
=>\(\dfrac{9}{16}IP^2=9.6^2\)
=>IP=12,8(cm)
=>IN=7,2(cm)
\(MN=\sqrt{7.2\cdot20}=12\left(cm\right)\)
\(MP=\sqrt{12.8\cdot20}=16\left(cm\right)\)
NP=7.2+12.8=20cm
b: \(S_{MIP}=\dfrac{9.6\cdot12.8}{2}=9.6\cdot6.4=61.44\left(cm^2\right)\)