Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì ∆MNP cân tại M
=> MN = MP , MNP = MPN
=> MNP = \(\frac{180°-NMP}{2}\)
Vì MQ = MK
=> ∆MQK cân tại M
=> MQ = MK , MKQ = MQK
=> QKM = \(\frac{180°-QMK}{2}\)
Mà QMK = NMP ( đối đỉnh)
=> QKM = MNP
Mà 2 góc này ở vị trí so le trong
=> QK//NP
=> QKPN là hình thang (1)
Ta có :
QM + MP = QP
KM + MN = KN
Mà QM = MK , MN = MP
=> OP = KN (2)
=> QKPN là hình thang cân
hì, bạn xem lại nốt đề câu b nữa nha... tại qua P vẽ đường thằng a song song với NP là không được á, đồng thời nếu vẽ thì cũng ko có cắt MP á
Bạn ơi, xem lại đề giúp mình nha. Tại mình thấy đề cho 2 lần MP mà 2 lần giá trị khác nhau á, một cái MP=6 một cái MP=1 hehe
Hình tự vẽ :(
Gọi \(Q\) là giao điểm của \(HK\) và \(MN\)
\(\Rightarrow KQ\) là đường trung tuyến của \(\Delta MNK\Rightarrow QM=QN\)
Xét \(\Delta MNI\) và \(\Delta KNM\) \(\left(\widehat{M}=\widehat{K}=90^o\right)\)
ta có: \(\widehat{N}\) là góc chung
\(\Rightarrow\Delta MNI\sim\Delta KNM\) \(\left(g-g\right)\)
mà \(\Delta KNM\) là tam giác vuông cân tại \(\widehat{K}\) \(\left(gt\right)\)
\(\Rightarrow\Delta MNI\) là tam giác vuông cân tại \(\widehat{M}\)
\(\Rightarrow MN=MI\) \(\Rightarrow MI=5\)
mà \(MK\) là đường cao của \(\Delta MNI\)
\(\Rightarrow MK\) cũng là trung tuyến của \(\Delta MNI\)
\(\Rightarrow KN=KI\)
Xét \(\Delta MNI\) ta có:
\(QN=QM\) \(\left(cmt\right)\)
\(KN=KI\) \(\left(cmt\right)\)
\(\Rightarrow QK\) là đường trung bình của \(\Delta MNI\)
\(\Rightarrow QK=\dfrac{MI}{2}=\dfrac{5}{2}\)
Xét \(\Delta MNP\) ta có:
\(QN=QM\) \(\left(cmt\right)\)
\(HN=HP\) (\(H\) là trung điểm của \(NP\))
\(\Rightarrow QH\) là đường trung bình của \(\Delta MNP\)
\(\Rightarrow QH=\dfrac{MP}{2}=\dfrac{13}{2}\)
Ta có \(QH=QK+HK\)
\(\Rightarrow HK=QH-QK=\dfrac{13}{2}-\dfrac{5}{2}=4\)
Vậy \(HK=4\)
Sửa đề:
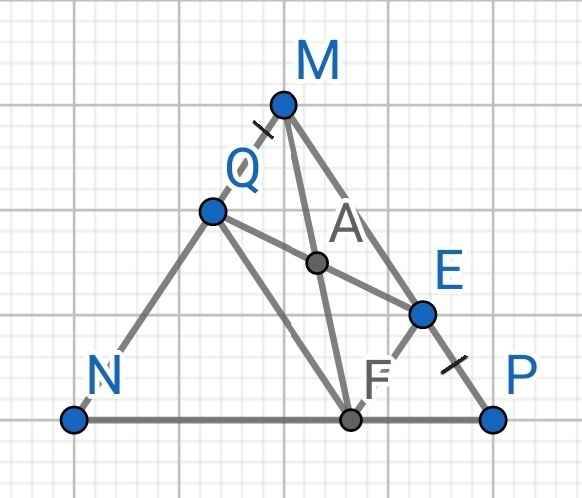
Cho tam giác MNP cân tại M, điểm Q nằm giữa M và N, lấy điểm E nằm giữa M và P sao cho MQ = PE. Từ Q kẻ đường thẳng song song MP cách NP ở F. Chứng minh:
a) Tứ giác MQFE là hình bình hành
b) Trung điểm của MF thuộc đường thẳng QE
GIẢI
a) Do ∆MNP cân tại M (gt)
⇒ MN = MP
Mà MQ = PE (gt)
⇒ MN - MQ = MP - ME
⇒ QN = ME
Do QF // MP (gt)
⇒ ∠QFN = ∠MPN (đồng vị) (1)
Mà ∆MNP cân tại M
⇒ ∠MPN = ∠MNP
⇒ ∠MPN = ∠QNF (2)
Từ (1) và (2) ⇒ ∠QFN = ∠QNF
⇒ ∆QNF cân tại Q
⇒ QN = QF
Mà QN = ME (cmt)
⇒ QF = ME
Do QF // MP (gt)
⇒ QF // ME
Tứ giác MQFE có:
QF // ME (cmt)
QF = ME (cmt)
⇒ MQFE là hình bình hành
b) Gọi A là trung điểm của MF
Do MQFE là hình bình hành
⇒ A là trung điểm của hai đường chéo MF và QE
⇒ A là trung điểm của QE
⇒ A ∈ QE
cho tam giác MNP vuông tại M có MN=4cm;MP=3cm
a)tính đọ dài NP và so sánh các góc của tam giác MNP
b)Trên tia đối tia PM lấy A sao cho P là trung điểm của đoạn thẳng AM.QUa P dựng đường thẳng vuông góc với AM cắt AN tại C.C/m tam giác CPM=tam giác CPA
c)C/m CM=CN
d)GỌi G là giao điểm của MC và NP.TÍnh NG
e)Từ A vẽ đường thẳng vuông góc với NP tại D.Vẽ tia Nx là tia phân giác của góc MNP,vẽ tia Ay là tian pg của PAD,tia Ay cắt các tia NP,Nx,NM lần lượt tại E,H,K.C/m tam giác NEK cân
Mình thấy đề sao sao á
Phần câu hỏi theo mình phải là QN/QP chứ nhỉ