NN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
PT
1
14 tháng 8 2023
a: Xét ΔAMN và ΔAPE có
AN=AE
MN=PE
AM=AP
=>ΔAMN=ΔAPE
b: ΔAMN=ΔAPE
=>góc NMA=góc EAP
=>góc NMA=góc AMP
=>MA là phân giác của góc NMP
2 tháng 1 2022
b: Xét ΔMND và ΔMPD có
MN=MP
ND=PD
MD chung
Do đó: ΔMND=ΔMPD
21 tháng 3 2023
a: Xét ΔMNK và ΔMEK có
MN=ME
góc NMK=góc EMK
MK chung
=>ΔMNK=ΔMEK
b,c: Xét ΔKNF và ΔKEP có
KN=KE
góc KNF=góc KEP
NF=EP
=>ΔKNF=ΔKEP
=>KF=KP
d: ΔKNF=ΔKEP
=>góc NKF=góc EKP
=>góc EKP+góc PKF=180 độ
=>F,K,E thẳng hàng
10 tháng 12 2021
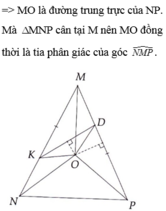
a) Xét tam giác MNP có: MN = MP (gt).
=> Tam giác MNP cân tại M.
=> Góc N = Góc P (Tính chất tam giác cân).
b) Xét tam giác MNP cân tại M:
MI là trung tuyến (I là trung điểm của cạnh NP).
=> MI là phân giác của góc NMP (Tính chất các đường trong tam giác).
c) Xét tam giác MNP cân tại M:
MI là trung tuyến (I là trung điểm của cạnh NP).
=> MI là đường cao (Tính chất các đường trong tam giác).
=> MI vuông góc với NP (đpcm).