Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔMBP vuông tại B và ΔMAN vuông tại A có
\(\widehat{BMP}\) chung
Do đó: ΔMBP\(\sim\)ΔMAN(g-g)
Suy ra: \(\dfrac{MB}{MA}=\dfrac{MP}{MN}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(MB\cdot MN=MA\cdot MP\)
b) Xét ΔMNP có
NA là đường cao ứng với cạnh MP(gt)
PB là đường cao ứng với cạnh MN(gt)
NA cắt PB tại H(gt)
Do đó: H là trực tâm của ΔMNP(Tính chất ba đường cao của tam giác)
Suy ra: MH\(\perp\)NP tại C

a: Xét ΔMIN vuông tại I và ΔMQP vuông tại Q có
góc M chung
=>ΔMIN đồng dạng với ΔMQP
c: Xét ΔMQI và ΔMPN có
MQ/MP=MI/MN
góc M chung
=>ΔMQI đồng dạng với ΔMPN

A B C E F H I
Giải
a) Xét \(\Delta BHF\) và \(\Delta CHE\) có:
\(\widehat{BHF}=\widehat{CHE}\) (vì đối đỉnh)
\(\widehat{BFH}=\widehat{CEH}=90^o\)
=> \(\Delta BHF\) s \(\Delta CHE\) (g - g)
b) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat{A}\) là góc chung
\(\widehat{AEB}=\widehat{AFC}=90^o\)
=> \(\Delta ABE\) s \(\Delta ACF\) (g - g)
=> \(\frac{AB}{AC}=\frac{AE}{AF}\)
=> AF . AB = AE . AC
c) Xét \(\Delta AEF\) và \(\Delta ABC\) có:
\(\widehat{A}\) là góc chung
\(\frac{AE}{AB}=\frac{AF}{AC}\) (vì \(\Delta ABE\) s \(\Delta ACF\))
=> \(\Delta AEF\)s \(\Delta ABC\) (c - g - c)
d) Câu d mình không nghĩ ra. Bạn tự làm nha, chắc là xét tam giác đồng dạng rồi suy ra hai góc bằng nhau và sẽ suy ra đường phân giác đó.

a: Xét ΔABM vuông tại M và ΔACN vuông tại N có
\(\widehat{BAM}\) chung
Do đó: ΔABM~ΔACN
b: Xét ΔPNB vuông tại N và ΔPMC vuông tại M có
\(\widehat{NPB}=\widehat{MPC}\)(hai góc đối đỉnh)
Do đó: ΔPNB~ΔPMC
=>\(\dfrac{PB}{PC}=\dfrac{NB}{MC}\)
=>\(PB\cdot MC=NB\cdot PC\)
c: Ta có; ΔAMB~ΔANC
=>\(\dfrac{AM}{AN}=\dfrac{AB}{AC}\)
=>\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
Xét ΔAMN và ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
\(\widehat{MAN}\) chung
Do đó: ΔAMN~ΔABC
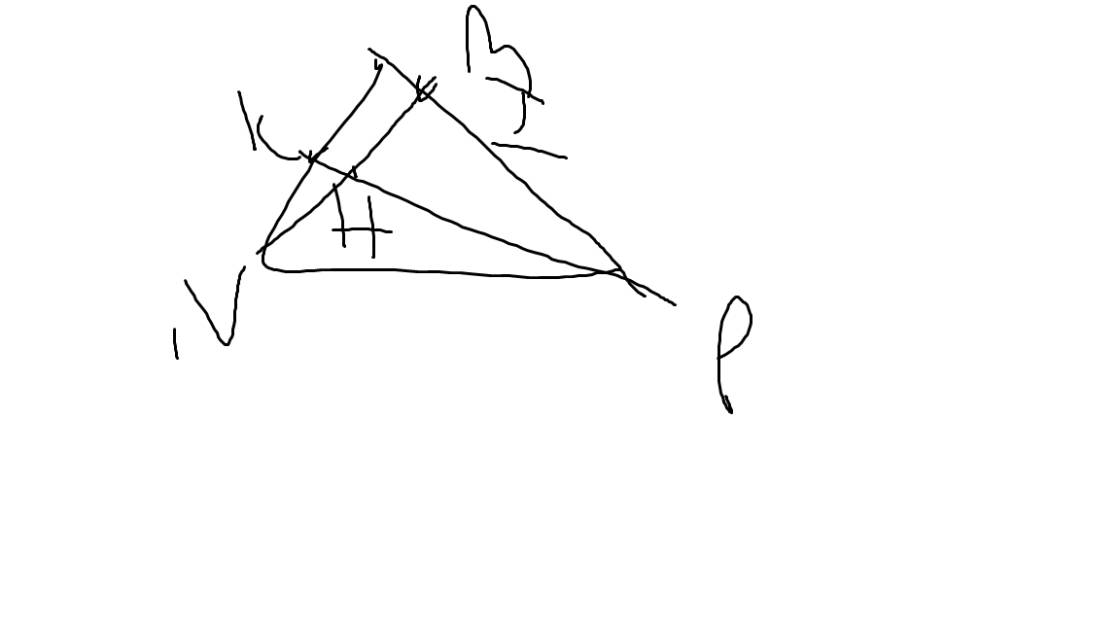
a: Xét ΔMIN vuông tại I và ΔMKP vuông tại K có
\(\widehat{IMN}\) chung
Do đó: ΔMIN~ΔMKP
b: Xét ΔHKN vuông tại K và ΔHIP vuông tại I có
\(\widehat{KHN}=\widehat{IHP}\)(hai góc đối đỉnh)
Do đó: ΔHKN~ΔHIP
=>\(\dfrac{HK}{HI}=\dfrac{HN}{HP}\)
=>\(HK\cdot HP=HN\cdot HI\)
c: Xét ΔMNP có
NI,PK là các đường cao
NI cắt PK tại H
Do đó: H là trực tâm của ΔMNP
=>MH\(\perp\)NP tại A
Xét ΔNAH vuông tại A và ΔNIP vuông tại I có
\(\widehat{ANH}\) chung
Do đó: ΔNAH~ΔNIP
=>\(\dfrac{NA}{NI}=\dfrac{NH}{NP}\)
=>\(NH\cdot NI=NA\cdot NP\)
Xét ΔPAH vuông tại A và ΔPKN vuông tại K có
\(\widehat{APH}\) chung
Do đó: ΔPAH~ΔPKN
=>\(\dfrac{PA}{PK}=\dfrac{PH}{PN}\)
=>\(PA\cdot PN=PH\cdot PK\)
\(NI\cdot NH+PK\cdot PH\)
\(=NA\cdot NP+PA\cdot PN=PN\left(NA+PA\right)=NP^2\)