Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét ΔMNP có
NQ là đường cao ứng với cạnh MP
PR là đường cao ứng với cạnh MN
MP cắt MN tại S
Do đó: MS\(\perp\)NP
b) Ta có: MS\(\perp NP\)(cmt)
nên \(\widehat{SMN}+\widehat{MNP}=90^0\)
hay \(\widehat{SMN}=25^0\)
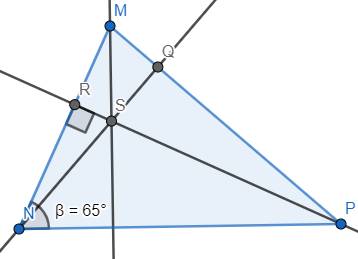
a) Theo đề ta có S là trực tâm của tam giác MNP và MNP là tam giác nhọn
Suy ra MS cũng là đường cao đáy NP, hay \(MS\perp NP\)
b) Gọi O là giao điểm của MS và NP. Ta có MNO là tam giác vuông tại O
Suy ra \(\widehat{MNO}+\widehat{NMO}=90^o\) hay \(\widehat{MNP}+\widehat{SMR}=90^o\)
Suy ra \(\widehat{SMR}=90^o-\widehat{MNP}=90^o-65^o=25^o\)
a) xét tam giác MHN và tam giác MHP có
\(\widehat{MHN}\) = \(\widehat{MHP}\)(= 90 ĐỘ)
MN = MP ( tam giác MNP cân tại M)
MH chung
=> tam giác MHN = tam giác MHP (cạnh huyền cạnh góc vuông)
b) vì tam giác MHN = tam giác MHP (câu a)
=> \(\widehat{M1}\)= \(\widehat{M2}\)(2 góc tương ứng)
=> MH là tia phân giác của \(\widehat{NMP}\)
bạn tự vẽ hình nhé
a.
vì tam giác MNP cân tại M=> MN=MP và \(\widehat{N}\)=\(\widehat{P}\)
Xét tam giác MHN và tam giác MHP
có: MN-MP(CMT)
\(\widehat{N}\)=\(\widehat{P}\)(CMT)
MH là cạnh chung
\(\widehat{MHN}\)=\(\widehat{MHP}\)=\(^{90^0}\)
=> Tam giác MHN= Tam giác MHP(ch-gn)
=> \(\widehat{NMH}\)=\(\widehat{PMH}\)(2 GÓC TƯƠNG ỨNG) (1)
và NH=PH( 2 cạnh tương ứng)
mà H THUỘC NP=> NH=PH=1/2NP (3)
b. Vì H năm giữa N,P
=> MH nằm giữa MN và MP (2)
Từ (1) (2)=> MH là tia phân giác của góc NMP
c. Từ (3)=> NH=PH=1/2.12=6(cm)
Xét tam giác MNH có Góc H=90 độ
=>\(MN^2=NH^2+MH^2\)( ĐL Py-ta-go)
hay \(10^2=6^2+MH^2\)
=>\(MH^2=10^2-6^2\)
\(MH^2=64\)
=>MH=8(cm)
