Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi S' là giao điểm của TV và FC
Ta sẽ chứng minh S trùng với S' bằng cách chứng minh HS' và HS cùng vuông góc với FC.
Thật vậy:
\(\Delta FTV\)cân tại F nên \(\widebat{FT}=\widebat{FV}\)
Do đó \(\widehat{FCV}=\widehat{FVS'}\)
Từ đó suy ra \(\Delta FCV~\Delta FVS'\left(g.g\right)\)
Suy ra \(FS'.FC=FV^2\)
Mà FV = FH nên \(FS'.FC=FH^2\)
Từ đó suy ra \(\Delta FS'H~\Delta FHC\left(c-g-c\right)\)
\(\Rightarrow\widehat{FS'H}=\widehat{FHC}=90^0\)
\(\Rightarrow HS'\perp FC\)
Dễ dàng chứng minh được \(HS\perp FC\)
Lúc đó thì S trùng S'
Vậy T, V, S thẳng hàng (đpcm)

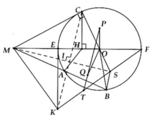
a, HS tự chứng minh
b, MH.MO = MA.MB ( = M C 2 )
=> ∆MAH:∆MOB (c.g.c)
=> M H A ^ = M B O ^
M B O ^ + A H O ^ = M H A ^ + A H O ^ = 180 0
=> AHOB nội tiếp
c, M K 2 = ME.MF = M C 2 Þ MK = MC
∆MKS = ∆MCS (ch-cgv) => SK = SC
=> MS là đường trung trực của KC
=> MS ^ KC tại trung của CK
d, Gọi MS ∩ KC = I
MI.MS = ME.MF = M C 2 => EISF nội tiếp đường tròn tâm P Þ PI = PS. (1)
MI.MS = MA.MB (= M C 2 ) => AISB nội tiếp đường tròn tâm Q Þ QI = QS. (2)
Mà IT = TS = TK (do DIKS vuông tại I). (3)
Từ (1), (2) và (3) => P, T, Q thuộc đường trung trực của IS => P, T, Q thẳng hàng

A B C T K O P S E F G I
a) Áp dụng tính chất của góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung, ta có:
\(\widehat{TAB}=\widehat{TCA}\)
Suy ra \(\Delta\)TAB ~ \(\Delta\)TCA (g.g) \(\Rightarrow\frac{TA}{TC}=\frac{TB}{TA}\Rightarrow TA^2=TB.TC\)(đpcm)
Hai điểm A và K cùng nằm trên (T) nên \(\Delta\)ATK cân tại T => \(\widehat{TAK}=\widehat{TKA}\)(1)
Dễ thấy góc TKA là góc ngoài của \(\Delta\)ACK => \(\widehat{TKA}=\widehat{CAK}+\widehat{ACK}\)
\(\Rightarrow\widehat{CAK}=\widehat{TKA}-\widehat{ACK}\)(2)
Ta có: \(\widehat{BAK}=\widehat{TAK}-\widehat{TAB}=\widehat{TAK}-\widehat{ACB}\)(Do \(\widehat{TAB}=\widehat{ACB}\))
hay \(\widehat{BAK}=\widehat{TAK}-\widehat{ACK}\)(3)
Từ (1); (2) và (3) suy ra: \(\widehat{BAK}=\widehat{CAK}\)=> AK là tia phân giác của \(\widehat{BAC}\)(đpcm).
b) Ta có: \(\frac{TA}{TC}=\frac{TB}{TA}\)=> \(\frac{TP}{TC}=\frac{TB}{TP}\)(P và A thuộc (T))
Từ đó ta chứng minh được: \(\Delta\)TBP ~ \(\Delta\)TPC (c.g.c) => \(\widehat{TPB}=\widehat{TCP}\)
Xét \(\Delta\)BPC: Tia PT nằm ngoài tam giác thỏa mãn \(\widehat{TPB}=\widehat{TCP}\)
Vậy nên TP là tiếp tuyến của đường tròn ngoại tiếp \(\Delta\)BPC (đpcm).
c) Gọi giao điểm của của AT và EF kéo dài là G, EF cắt AP tại điểm I.
Ta thấy tứ giác BEFC nội tiếp (O) => \(\widehat{BCP}=\widehat{EFP}\)hay \(\widehat{EFP}=\widehat{TCP}\)
Mà \(\widehat{TPB}=\widehat{TCP}\)(cmt) => \(\widehat{EFP}=\widehat{TPB}\)
Vì 2 góc trên nằm ở vị trí so le trong nên TP // EF hay TP // GI
Lại có: \(\Delta\)ATP cân tại T có GI // TP (G\(\in\)AT; I\(\in\)AP) => \(\Delta\)AGI cân tại G => \(\widehat{GAI}=\widehat{GIA}\)(4)
\(\widehat{EAI}=\widehat{GAI}-\widehat{GAE}\)(5); \(\widehat{FAI}=\widehat{GIA}-\widehat{AFG}\)(6)
Dễ chứng minh \(\widehat{GAE}=\widehat{AFG}\)(7)
Từ (4); (5); (6) và (7) => \(\widehat{EAI}=\widehat{FAI}\) hay \(\widehat{EAS}=\widehat{FAS}\)
Mà tứ giác AESF nội tiếp (O) => \(\widehat{EAS}=\widehat{EFS}\)và \(\widehat{FAS}=\widehat{FES}\)
Từ đó ta có: \(\widehat{EFS}=\widehat{FES}\)=> Tam giác ESF cân tại S => S nằm trên đường trung trực của EF
Mà EF là dây cung của (O) nên O cũng nằm trên trung trực của EF
Do đó SO là trung trực của EF hay \(SO\perp EF\)(đpcm).
Xin lỗi bạn, 2 góc EFP và TPB là hai góc đồng vị, không phải so le trong nhé.