Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác HGEN có
HG//EN
HN//GE
Do đó: HGEN là hình bình hành
mà HE là tia phân giác
nên HGEN là hình thoi

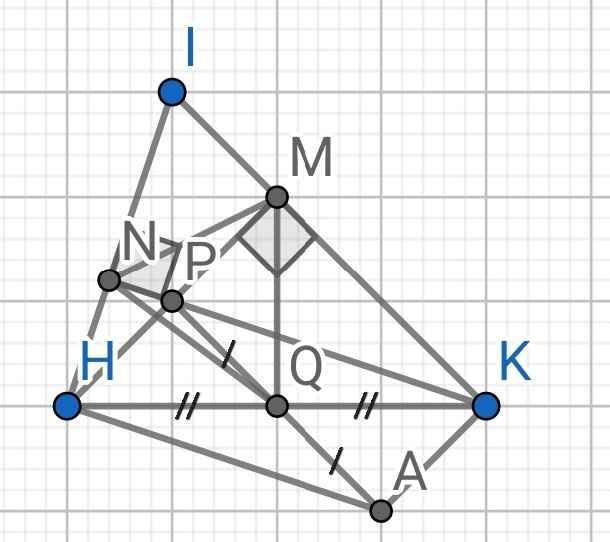 a) Do PQ = QA (gt)
a) Do PQ = QA (gt)
⇒ Q là trung điểm của AP
Tứ giác PHAK có:
Q là trung điểm của AP (cmt)
Q là trung điểm của HK (gt)
⇒ PHAK là hình bình hành
b) Do PHAK là hình bình hành (cmt)
⇒ PK = AH
c) ∆HNK vuông tại N
Q là trung điểm của HK (gt)
⇒ NQ là đường trung tuyến ứng với cạnh huyền HK
⇒ NQ = HK : 2 (1)
∆HMK vuông tại M
Q là trung điểm HK (gt)
⇒ MQ là đường trung tuyến ứng với cạnh huyền HK
⇒ MQ = HK : 2 (2)
Từ (1) và (2) ⇒ MQ = NQ
∆MNQ có:
MQ = NQ (cmt)
⇒ ∆MNQ cân tại Q

a: Xét ΔHIK có IN là phân giác
nên HN/NK=HI/IK=HK/IK(1)
Xét ΔHIK có KM là phân giác
nên HM/MI=HK/KI(2)
Từ (1) và (2) suy ra HN/NK=HM/MI
=>MN//IK
=>ΔHMN\(\sim\)ΔHIK
b: Ta có: HN/HI=NK/IK
=>HN/10=NK/8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{HN}{5}=\dfrac{NK}{4}=\dfrac{HN+NK}{5+4}=\dfrac{10}{9}\)
Do đó: HN=50/9(cm)
Xét ΔHIK có MN//IK
nên MN/IK=HN/HK
\(\Leftrightarrow MN=\dfrac{50}{9}:10\cdot8=\dfrac{40}{9}\left(cm\right)\)

a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành
B A C D E K

a) Ta có: E và M đối xứng với nhau qua D
=> DE = DM ; ME vuông góc AB
Ta có BD = DA ( D là trun điểm AB )
mà ME vuông góc AB ( cmt )
=> AB là trung trực của ME hay E và M đối xứng nhau qua D
b) Xét Tam giác ABC có:
M là trung điểm BC ( gt )
D là trung điểm AB ( gt)
=> DM là đường trung bình tam giác ABC
=> DM // AC; DM = 1/2AC
mà E thuộc DM
nên EM // AC
Xét tứ giác AEMC có:
EM // AC ( cmt)
EM = AC ( cùng = 2DM )
=> Tứ giác AEMC là hình bình hành( tứ giác có 2 cạnh đối vừa // vừa = nhau là hình bình hành)
c) Xét tứ giác AEBM có:
ED = DM ( gt )
DB = AD ( gt )
=> Tứ giác AEBM là hình bình hành ( D/h 5 )
mà AB vuông góc EM
=> hbh AEBM là hình thoi ( D/h 3 )
d) Ta có : AM = 1/2BC ( trung tuyến ứng với cạnh huyền)
=> AM = 1/2 . BC = 1/2. 5 = 2,5 (cm)
Chu vi hình thoi AEBM:
2,5 . 4 =10 (cm)