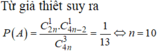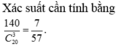Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Cách 1:
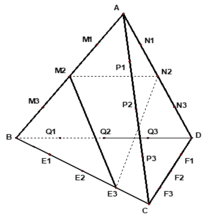
Gọi các điểm được đánh dấu để chia đều các cạnh của tứ diện đều ABCD như hình vẽ.
+ Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Số phần tử của S là số cách chọn ra 3 điểm không thẳng hàng trong số 18 điểm đã cho.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Chọn ra 3 điểm thẳng hàng trong 18 điểm trên có 6. C 6 3 = 6 cách.
Suy ra số tam giác thỏa mãn là C 18 3 - 6 = 810
+ Gọi T là tập hợp các tam giác lấy từ ABCD sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện ABCD.
- Chọn 1 cạnh của tứ diện để mặt phẳng chứa tam giác chỉ song song với đúng cạnh đó: có C 6 1 cách.
Xét các tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD, suy ra tam giác đó phải có một cạnh song song với BD.
- Có 6 cách chọn cạnh song song với BD là
![]()
- Giả sử ta chọn cạnh M 2 N 2 là cạnh của tam giác. Cần chọn đỉnh thứ 3 của tam giác trong 16 điểm còn lại.
Do M 2 N 2 ⊂ (ABD) mà mặt phẳng chứa tam giác song song với BD nên đỉnh thứ 3 không thể là 7 điểm còn lại nằm trong mp(ABD).
Do mặt phẳng chứa tam giác chỉ song song với BD nên đỉnh thứ 3 không được trùng với một trong ba điểm E 2 , F 2 , P 2 . Vậy đỉnh thứ 3 chỉ được chọn trong 16 -7 - 3 = 6 điểm còn lại.
Suy ra có 6 tam giác có 1 cạnh là M 2 N 2 và mặt phẳng chứa nó chỉ song song với BD.
Vậy số tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD là: 6.6 = 36.
Tương tự cho các trường hợp khác, ta có số tam giác mà mặt phẳng chứa nó chỉ song song với đúng một cạnh của tứ diện ABCD là: 36.6 = 216.
Vậy xác suất cần tìm là
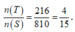
Cách 2: Lưu Thêm
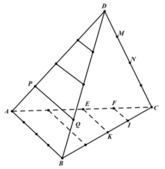
+) Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Trong số C 18 3 đó, có 6 cách chọn ra 3 điểm thẳng hàng trên các cạnh.
Suy ra n(S) = C 18 3 - 6 = 810
+) Xét phép thử: “Lấy ngẫu nhiên một phần thử thuộc S”. Ta có ![]()
+) Gọi T là biến cố: “Mặt phẳng chứa tam giác được chọn song song với đúng một cạnh của tứ diện đã cho”.
Chọn một cạnh của tứ diện: 6 cách, (giả sử chọn AB).
Chọn đường thẳng song song với AB: 6 cách, (giả sử chọn PQ).
Chọn đỉnh thứ 3: 6 cách, (M, N, E, K, F, I).
Suy ra n(T) = 6.6.6 = 216
Vậy 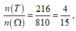

Đáp án B
Số phần tử của tập hợp M là: C 15 3
Gọi O là tâm đường tròn ngoại tiếp của đa giác đều, Xét một đỉnh A bất kỳ của đa giác: Có 7 cặp đỉnh của đa giác đối xứng với nhau qua đường thẳng OA, hay có 7 tam giác cân tại đỉnh A. Như vậy, với mỗi một đỉnh của đa giác có 7 tam giác nhận nó làm đỉnh tam giác cân.
Số tam giác đều có 3 đỉnh là các đỉnh của đa giác là 15 3 = 5 tam giác.
Tuy nhiên, trong các tam giác cân đã xác định ở trên có cả tam giác đều, do mọi tam giác đều thì đều cân tại 3 đỉnh nên tam giác đều được đếm 3 lần.
Suy ra, số tam giác cân nhưng không phải tam giác đều có 3 đỉnh là 3 đỉnh của đa giác đã cho là: 7.15 – 3.5 = 90
Do đó xác suất cần tìm là P = 90 C 15 3 = 18 91 .

Chọn B
Các số tự nhiên của tập X có dạng a b c d e ¯ , suy ra tập X có 9. 10 4 số. Lấy từ tập X ngẫu nhiên hai số có C 90000 2 số.
Vì ![]()
![]() có 25 số.
có 25 số.
Suy ra số tự nhiên có năm chữ số chia hết cho 4 là 9.10.10.25 = 22500 số.
Số tự nhiên có năm chữ số không chia hết cho 4 là 9.10.10.75 = 67500 số.
Vậy xác suất để ít nhất một số chia hết cho 4 là: 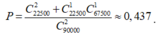

SỐ tam giác tạo được từ 3 đỉnh là \(C^3_{12}\)
Số tam giác có 3 đỉnh là 3 đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn
=>Có 12 tam giác
Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác
=>CÓ 8*12=96 tam giác
=>\(P=\dfrac{C^3_{12}-12-12\cdot8}{C^3_{12}}\)

Chọn C
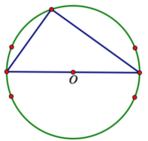
Đa giác đều nội tiếp một đường tròn tâm O. Lấy ngẫu nhiên 3 đỉnh có C 20 3 cách.
Để 3 đỉnh là 3 đỉnh một tam giác vuông không có cạnh nào là cạnh của đa giác đều thực hiện theo các bước:
Lấy một đường kính qua tâm đường tròn có 10 cách ta được 2 đỉnh.
Chọn đỉnh còn lại trong 20 - 2 - 4 = 14 đỉnh (loại đi 2 đỉnh thuộc đường kính và 4 đỉnh gần ngay đường kính đó) cách.
Vậy có tất cả 10.14 = 140 tam giác thoả mãn.

Xác suất cần tính bằng 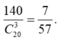

Đáp án C
+) Số tam giác được tạo từ 3 đỉnh trong 12 đỉnh: C 12 3
+) Số tam giác có 3 đỉnh là đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn đề bài, nên có 12 tam giác
+) Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác: cứ 1 cạnh, trừ đi 2 đỉnh kể, còn 8 đỉnh, với 2 đỉnh đầu mút của cạnh đó cho 1 tam giác thỏa mãn đề bài, nên có 8.12 tam giác
Vậy số tam giác có 3 đỉnh là đỉnh của đa giác và không có cạnh nào là cạnh của đa giác là C 12 3 - 12 - 12 . 8
Vậy kết quả là C 12 3 - 12 - 12 . 8 C 12 3

Đáp án C

Gọi A là biến cố: “Chọn được tam giác vuông”
Đa giác đều 4n đỉnh nội tiếp trong đường tròn tâm O có 2n đường chéo qua tâm O .
Mỗi tam giác vuông tạo bởi hai đỉnh nằm trên cùng một đường chéo qua tâm O và một đỉnh trong 4 n - 2 đỉnh còn lại.
Suy ra số tam giác vuông được tạo thành là C 2 n 1 . C 4 n - 2 1 .