Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này khá căn bản thôi do tam giác ABC đều
`=>hatA=hatB=hatC=60^o`
`\hat{BOC}` là góc ở tâm nên gấp 2 lần góc nội tiếp
`=>hat{BOC}=2hatA=120^o`
Vì `hat{OBM}=hat{OCM}=90^o`(do các tt lần lượt lại B,C)
`hat{BOC}+hat{OBM}+hat{OCM}+hat{BMC}=360^o`( đây là tứ giác)
`=>hat{BMC}=360^o-(hat{BOC}+hat{OBM}+hat{OCM}+hat{BMC})=60^o`

khi tia OA cắt đường tròn tâm O tại D nên AD là đường kính chia ra 2 cung AD bằng nhau
mà tam giác ABC cân tại A có góc ABC =góc ACB là 2 góc nội tiếp chắc 2 cung AB và AC nên cung AB=cung AC
cung AD=cung AB+cung BD
cung AD=cung AC+cung CD
ta có cung AD=cung AD,cung AB=AC=>cung BD=cung CD
theo đề bài số đo cung nhỏ BD=cung BD+cung CD=>100=2 cung CD=>cung CD bằng 50 độ
MÀ GÓC COD là góc ở tâm chắc cung CD
NÊN SUY RA ĐƯỢC GÓC COD BẰNG 50 ĐỘ

Bạn mở trong đường link này sẽ có https://moon.vn/hoi-dap/cho-tam-giac-deu-abc-noi-tiep-trong-duong-tron-tam-o-goi-mnp-lan-luot-la-trung-diem--665623
A B C F G N O E
( Hình hơi bị lệch một xíu, tam giác không chính xác lắm nha)
a) Do tam giác ABC đều và M, N lần lượt là trung điểm của \(AB,BC\Rightarrow\hept{\begin{cases}OM\perp AB\\ON\perp BC\end{cases}\Rightarrow\widehat{OMB}=\widehat{ONB}=90^o}\)
Xét tứ giác BMON có: \(\widehat{OMB}+\widehat{ONB}=180^o\) suy ra tứ giác BMON là tứ giác nội tiếp (tứ giác cỏ tổng 2 góc đối bằng 180o
b) Do O là trọng tâm tam giác ABC(giả thiết) suy ra \(ON=\frac{OA}{2}=\frac{R}{2}\)( tính chất đường trung tuyến).
Mặt khác, \(OG=ON+NG\Rightarrow NG=OG-ON=R-\frac{R}{2}=\frac{R}{2}\)
Vậy \(NO=NG=\frac{R}{2}\left(đpcm\right)\)
c) Gọi \(E=EC\Omega PN\) ta có: \(OC\perp AB\) (do tam giác ABC đều); \(NO//AB\)( NP là đường trung bình của tam giác ABC)
\(\Rightarrow OC\perp NP\) tại E => tam giác OEF vuông tại E.
Xét tam giác ONC vuông tại N có đường cao NE ta có: \(ON^2=OE.OC\Rightarrow OE=\frac{ON^2}{OC}=\frac{R}{4}\) (hệ thức lượng)
Xét tam giác vuông OEF có: \(\sin\widehat{OFE}=\sin\widehat{OFP}=\frac{OE}{OF}=\frac{R}{\frac{4}{R}}=\frac{1}{4}\Rightarrow\widehat{OFP}\approx14^O28'\)

a: sđ cung nhỏ AB=2*30=60 độ
sđ cung lớn AB là 360-60=300 độ
góc PAB=góc BCA=30 độ
góc AOB=sđ cung nhỏ AB=60 độ
b,c: Bạn ghi lại đề đi bạn
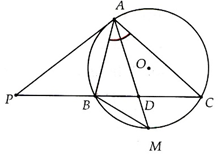
đây nhé bạn