Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác đều ABC độ dài cạnh là 6cm. Kẻ AI vuông góc với BC. Độ dài cạnh AI là:
A. 3√3 cm
B. 3 cm
C. 3√2 cm
D. 6√3 cm

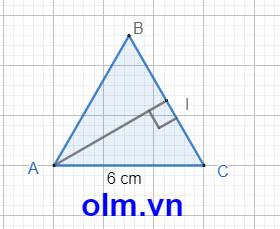
IC = \(\dfrac{1}{2}\)BC (vì trong tam giác đều đường cao cũng là trung tuyến, đường trung trực, đường phân giác của tam giác đó).
IC = 6 \(\times\) \(\dfrac{1}{2}\) = 3 (cm)
Xét \(\Delta\)AIC vuông tại C nên theo pytago ta có:
AI2 = AC2 - IC2 = 62 - 32 = 27 (cm)
AI = \(\sqrt{27}\) = 3\(\sqrt{3}\)(cm)
Chọn A. 3\(\sqrt{3}\)cm

a: Ta có: ΔABC cân tại A
mà AI là đường trung tuyến
nên AI là đường cao
b: Ta có: I là trung điểm của BC
nên IB=IC=4cm
Xét ΔAIB vuông tại I có
\(AB^2=AI^2+BI^2\)
hay \(AB=2\sqrt{13}\left(cm\right)\)
c: Xét ΔAMI vuông tại M và ΔANI vuông tại N có
AI chung
\(\widehat{MAI}=\widehat{NAI}\)
Do đó; ΔAMI=ΔANI
Suy ra; IM=IN
d: Xét ΔABC có
AM/AB=AN/AC
Do đó: MN//BC
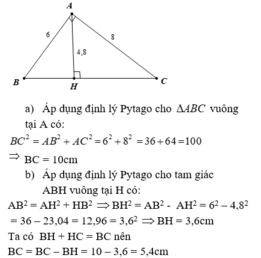
Hình bạn tự vẽ nhá :v
Vì tam giác ABC là tam giác đều
=> AI vừa là đường cao , vừa là đường trung tuyến ứng với BC
=> I là trung điểm BC
=> IC = 6:2 = 3 cm
Xét tam giác AIC vuông tại I
Áp dụng định lí Pitago , ta có :
AI2 = IC2 + AC2
=> AI2 = 32 + 62 = 9+36 = 45
=> AI = √45 ( vì độ dài AI luôn dương)