Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
Phương án A: 
nên 
nên đẳng thức ở phương án A là đúng.
Phương án B: 
nên 
nên đẳng thức ở phương án B là đúng.
Phương án C:
Do đó: 
nên phương án C là đúng.
Dựng điểm D sao cho H là trung điểm AD.
Ta có; H là trung điểm của mỗi đường AD ; BC. Do đó, tứ giác ACDB là hình bình hành.
Do tam giác ABC là tam giác đều nên đường cao AH đồng thời là đường trung tuyến nên H là trung điểm BC: B H = H C = B C 2
Đáp án B
Do tam giác ABC là tam giác đều có AH là đường cao nên đồng thời là đường phân giác .
Suy ra: B A H ^ = 1 2 B A C ^ = 30 0 ; A B C ^ = 60 0 ; A H C ^ = 90 0
Do đó, sin B A H ^ = 1 2 ; c os B A H ^ = 3 2 . Do đó A sai; B sai.
Ta có A B C ^ = 60 0 ⇒ sin A B C ^ = 3 2 . Do đó C đúng.
Chọn C.
Chọn C.
Do tam giác cân tại A, AH là đường cao nên H là trung điểm BC.
Xét các đáp án:
+ Đáp án A. Ta có 
+ Đáp án B. Ta có 
+ Đáp án C. Ta có 
( H là trung điểm BC).
+ Đáp án D. Do 
không cùng hướng nên 
.
Chọn C.
Độ dài các cạnh của tam giác là a thì độ dài các vectơ
Chọn C.
Phương án A: do
nên loại A
Phương án B: do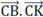
= CB. CK.cos00
= a2/2 nên loại B và D
Phương án C: do
Chọn C.