K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

18 tháng 7 2019
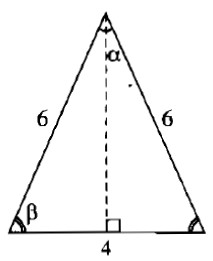
Vì các cạnh của tam giác lần lượt là 4cm, 6cm và 6cm nên tam giác đó là tam giác cân. Góc nhỏ nhất của tam giác là góc đối diện với cạnh 4cm.
Kẻ đường cao từ đỉnh của góc nhỏ nhất. Đường cao chia cạnh đáy thành hai phần bằng nhau mỗi phần 2cm.
Ta có: cosβ=26=13⇒β≈70∘32′cosβ=26=13⇒β≈70∘32′
Suy ra: α=180∘–(β+β)=180∘–2.70∘32'=38∘56′α=180∘–(β+β)=180∘–2.70∘32′=38∘56′
Vậy góc nhỏ nhất của tam giác bằng 38∘56′38∘56′.