Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét tam giác EAD và tam giác FAD có
AED=AFD=90*
EAD=FAD(gt)
AD chung
=> tam giác EAD= tam giác FAD(ch-gn)
=> DE=DF( 2 cạnh t.ứ) và EDA=FDA( 2 góc t,ứ)
Ta có EDA=FDA=30*=>EDF=EDA+FDA=30*+30*=60*
b. Tam giác EAD=tam giác FAD(ch-gn=>AE=AF
Mà KE=FI => AE+EK=AF+FI => AK=AI
Xét tam giác AKD và tam giác AID
AK=AI; KAD=IAK; AD chung
=> tam giác AKD= tam giác AID(cgc)
=> DK=DI
c. Ta có BAC+CAM=180*( kề bù)
=> 120* + CAM=180* => CAM= 60*
Lại có AD//MC=> DAC=ACM= 1/2BAC= 60*
Xét tam giác ACM có ACM= CAM=60*=> tam giác ACM đều => ACM=CAM=AMC=60*

A B C D E F K I
a,VÌ AD là p/g của ^A nên ^EAD = ^IAD = \(\frac{1}{2}\)^ EAI = \(\frac{1}{2}\cdot60^o=30^o\)
Xét tam giác vuông EAD và tam giác vuông IAD ta có: ^EAD = ^IAD ; chung AD
Nên tam giác vuông AED = tam giác vuông IAD (cạnh huỳen - góc nhọn)
do đó DE = DF (2 cạnh tương ứng) nên tam giác DEF cân tại D \(\left(1\right)\)
Do đó ^ADE = ^IDA =\(30^o\)mà ^EDI = ^ADE + ^IDA = \(30^o+30^o=60^o\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\)-> tam giác DEF đều. (ĐPCM)
b, Xét tam giác vuông DEF và tam giác vuông DEI, ta có: DE = DF ; KE = FI
nên tam giác vuông DEF = tam giác vuông DEI (2 cạnh góc vuông)
do đó DK = DI (2 cạnh tương ứng)
Nên tam giác DKI cân tại D (ĐPCM)

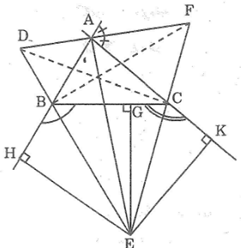
a. Ta có: E thuộc tia phân giác của ∠(CBH)
Suy ra: EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của ∠(BCK)
Suy ra: EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK.
b. Ta có: EH = EK (chứng minh trên)
Suy ra: E thuộc tia phân giác của ∠(BAC).
Mà E khác A nên AE là tia phân giác của ∠(BAC)
c. Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc trong tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.
d. Tương tự câu a, ta có:
BF là tia phân giác của ∠(ABC)
CD là tia phân giác của ∠(ACB)
Vậy AE, BF, CD là các đường phân giác của tam giác ABC.
e. Ta có: BF là tia phân giác góc trong tại đỉnh B
BE là tia phân giác góc trong tại đỉnh B
Suy ra: BF ⊥ BE (tính chất hai góc kề bù)
Vậy BF ⊥ ED.
Lại có: CD là đường phân giác góc trong tại C
CE là đường phân giác góc trong tại C
Suy ra: CD ⊥ CE (tính chất hai góc kề bù)
Vậy CD ⊥ EF.

ˆA=12A^=12 sđ BCBC⏜ (tính chất góc nội tiếp)
⇒⇒ sđ BCBC⏜ =2ˆA=2.320=640=2A^=2.320=640
BC = BE (gt)
⇒⇒ sđ BCBC⏜ = sđ BEBE⏜ = 640
ˆB=12B^=12 sđ ACAC⏜ (tính chất góc nội tiếp)
⇒⇒ sđ ACAC⏜ =2ˆB=2.840=1680=2B^=2.840=1680
AC = CF (gt)
⇒⇒ sđ CFCF⏜ = sđ ACAC⏜ = 1680
sđ ACAC⏜ + sđ AFAF⏜ + sđ CFCF⏜ = 3600
⇒⇒ sđ AFAF⏜ =3600–=3600– sđ ACAC⏜ – sđ CFCF⏜ = 3600 – 1680. 2 = 240
Trong ∆ABC ta có: ˆA+ˆB+ˆC=1800A^+B^+C^=1800

Bài 1:
Số đo góc ngoài tại đỉnh C là \(74^0+47^0=121^0\)
Câu 2:
Đặt \(\widehat{D}=a;\widehat{E}=b\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=52\\a+b=140\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=96\\b=44\end{matrix}\right.\)
Bài 3:
Theo đề, ta có: x+2x+3x=180
=>6x=180
=>x=30
=>\(\widehat{A}=30^0;\widehat{B}=60^0;\widehat{C}=90^0\)
Đề bài chưa đầy đủ, mình sẽ phản hồi lại khi có đủ đề bài. (Cụ thể hơn, giao điểm của DI và EK là gì? Có thể chụp hình vẽ lên không vậy bạn?