Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác DAB và tam giác DHB:
góc DAB= góc DHB =90o
DB chung
góc DBA= góc DBH
=> tam giác DAB = tam giác DHB (cạnh huyền _góc nhọn)
=> DA=DH (2 cạnh tương ứng)
b)
Ta có: DA = DH (cmt) (1)
và trong tam giác CHD :
DH là cạnh góc vuông
DC là cạnh huyền
=> DH < DC (2)
Từ (1) và (2) => AD < DH
c) Xét tam giác DAK và tam giác DHC:
góc DAK = góc DHC = 90o
DA = DH (cmt)
góc KDA = góc CDH (đối đỉnh)
=> tam giác DAK = tam giác DHC (cạnh góc vuông_ góc nhọn)
=> AK = HC (2 cạnh tương ứng)
Ta có: AB = HB (do tam giác DAB = tam giác DHB)
và AK = HC (cmt)
mà BK = AB + AK
BC = HB + HC
=> BK = BC
=> tam giác KBC cân
Cô nêu cách trình bày khác của câu c nhé. :)
Xét tam giác KBC, có KH, CK là các đường cao nên D là trực tâm của tam giác KBC. Từ đó suy ra BD là đường cao của tam giác KBC. Mà BD lại là đường phân giác nên tam giác KBC cân tại B.

a: Xet ΔDME và ΔDNF có
DM=DN
góc MDE chung
DE=DF
=>ΔDME=ΔDNF
=>EM=FN và góc DEM=góc DFN
b: Xet ΔNEF và ΔMFE có
NE=MF
EF chung
NF=ME
=>ΔNEF=ΔMFE
=>góc KEF=góc KFE
=>KE=KF
c: ΔDEF cân tại D
mà DH là đường cao
nên DH là trung tuyến
Xét ΔDEF có
DH,FN,EM là trung tuyến
=>DH,FN,EM đồng quy

a) Áp dụng định lí Pytago vào ΔDEF vuông tại D, ta được:
\(EF^2=DE^2+DF^2\)
\(\Leftrightarrow EF^2=9^2+12^2=225\)
hay EF=15(cm)
Vậy: EF=15cm

a) Xét tam giác DEH và tam giác DFH ta có:
DE = DF ( tam giác DEF cân tại D )
DEH = DFH ( tam giác DEF cân tại D )
EH = EF ( H là trung điểm của EF )
=> tam giác DEH = tam giác DFH ( c.g.c) (dpcm)
=> DHE=DHF(hai góc tương ứng)
Mà DHE+DHF=180 độ =>DHE=DHF=180 độ / 2 = 90 độ ( góc vuông ) hay DH vuông góc với EF ( dpcm )
b) Xét tam giác MEH và tam giac NFH ta có:
EH=FH(theo a)
MEH=NFH(theo a)
=> tam giác MEH = tam giác NFH ( ch-gn)
=> HM=HN ( 2 cạnh tương ứng ) hay tam giác HMN cân tại H ( dpcm )
c) Ta có : +) DM+ME=DE =>DM=DE-ME
+) DN+NF=DF => DN=DF-NF
Mà DE=DF(theo a) ; ME=NF( theo b tam giác MEH=tam giác NFH)
=>DM=DN => tam giác DMN cân tại D
Xét tam giac cân DMN ta có:
DMN=DNM=180-MDN/2 (*)
Xét tam giác cân DEF ta có:
DEF=DFE =180-MDN/2 (*)
Từ (*) và (*) Suy ra góc DMN = góc DEF
Mà DMN và DEF ở vị trí đồng vị
=> MN//EF (dpcm)
d) Xét tam giác DEK và tam giác DFK ta có:
DK là cạnh chung
DE=DF(theo a)
=> tam giác DEK= tam giác DFK(ch-cgv)
=>DKE=DKF(2 góc tương ứng)
=>DK là tia phân giác của góc EDF (1)
Theo a tam giac DEH= tam giac DFH(c.g.c)
=>EDH=FDH(2 góc tương ứng)
=>DH là tia phân giác của góc EDF (2)
Từ (1) và (2) Suy ra D,H,K thẳng hàng (dpcm)

\(\text{#TNam}\)
`a,` Xét Tam giác `HED` và Tam giác `HFD` có
`DE = DF (\text {Tam giác DEF cân tại D})`
\(\widehat{E}=\widehat{F}\) `(\text {Tam giác DEF cân tại D})`
`=> \text {Tam giác HED = Tam giác HDF (ch-gn)}`
`b,` Vì Tam giác `HED =` Tam giác `HFD (a)`
`-> HE = HF (\text {2 cạnh tương ứng})`
Xét Tam giác `HEM` và Tam giác `HFN` có:
`HE = HF (CMT)`
\(\widehat{E}=\widehat{F}\) `(a)`
\(\widehat{EMH}=\widehat{FNH}=90^0\)
`=> \text {Tam giác HEM = Tam giác HFN (ch-gn)}`
`-> EM = FN (\text {2 cạnh tương ứng})`
Ta có: \(\left\{{}\begin{matrix}DE=MD+ME\\DF=ND+NF\end{matrix}\right.\)
Mà `DE = DF, ME = NF`
`-> MD = ND`
Xét Tam giác `DMN: DM = DN (CMT)`
`-> \text {Tam giác DMN cân tại D}`
`->`\(\widehat{DMN}=\widehat{DNM}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `DEF` cân tại `D`
`->`\(\widehat{E}=\widehat{F}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{DMN}=\widehat{E}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {MN // EF (t/c 2 đt' //)}`

2) A B C D K H
a) Xét 2 tam giác DHB và tam giác DAB có:
\(\widehat{DAB}=\widehat{DHB}\)
DB là cạnh chung
\(\widehat{ABD}=\widehat{HBD}\)
\(\Rightarrow\Delta DAB=\Delta DHB\left(g-c-g\right)\)
\(\Rightarrow AD=DH\)
b) AB=BH (\(\Delta ADB=\Delta DBH\)
=> tam giác ABH cân tại B ( DB là đường p/g; đường trung tuyến )
=> \(\widehat{KDB}=\widehat{CDB}\)( \(\widehat{CDH}=\widehat{KDA}\)đối đỉnh)
=> \(\widehat{HDB}=\widehat{ADB}\)(theo câu a)
\(\Rightarrow\Delta KDA=\Delta CDH\left(g-c-g\right)\Rightarrow CH=KA\)
=> cạnh CD> cạnh AD (vì CD là cạnh huyền
c) HB=BA và CH=KA
=> KB=BC => tam giác KBC cân tại B

a: góc MDH=90 độ-góc DMH
=90 độ-2*góc MDF
=90 độ-2*góc E
=góc F+góc E-2*góc E
=góc F-gócE
b: (EF+DH)^2-(DF+DE)^2
=EF^2+2*EF*DH+DH^2-DF^2-DE^2-2*DF*DE
=DH^2>0
=>EF+DH>DF+DE
=>EF-DE>DF-DH
Lời giải:
Xét tam giác $DEH$ và $DFH$ có:
$DE=DF$ có $DEF$ cân tại $D$
$DH$ chung
$\widehat{DHE}=\widehat{DHF}=90^0$
$\Rightarrow \triangle DEH=\triangle DFH$ (ch-cgv)
$\Rightarrow EH=FH$
Xét tam giác $MHE$ và $MHF$ có:
$\widehat{MHE}=\widehat{MHF}=90^0$
$MH$ chung
$EH=FH$ (cmt)
$\Rightarrow \triangle MHE=\triangle MHF$ (c.g.c)
$\Rightarrow ME=MF$
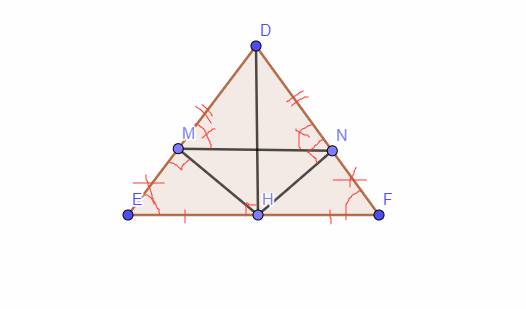
Hình vẽ: