Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét tam giác DIE và tam giác DIF
Có DI chung
IE=IF (GT)
DE=DF ( vì tam giác DEF cân tại D)
suy ra tam giác DIE =tam giác DIF (c.c.c)
suy ra góc EDI= góc FDI (hai góc tương tứng)
c) Xét tam giác vuông DMI và tam giác vuông DIN
có DI chung, góc EDI= góc FDI (CMT)
suy ra tam giác DMI = tam giác DIN (cạnh huyền-góc nhọn)
suy ra DM=DN suy ra tam giác DMN cân tại D
suy ra góc DMN = góc DNM (2)
suy ra góc MDN +góc DMN + góc DNM =1800 (3)
Từ (2) và (3) suy ra góc MDN +góc DMN + góc DMN =1800
suy ra góc MDN +2.góc DMN =1800suy ra góc DMN=(1800-góc MDN ) :2 (4)
LẠi có tam giác DEF cân tại D
suy ra góc DEF= góc DFE (5)
suy ra góc EDF +góc DEF + góc DFE =1800 (6)
Từ (5) và (6) suy ra góc EDF +góc DEF + góc DEF =1800
suy ra góc EDF +2.góc DEF =1800suy ra góc DEF=(1800-góc EDF ) :2 (7)
Từ (4) và (7) suy ra góc DMN = góc DEF
mà góc DMN đồng vị với góc DEF
suy ra MN//EF
d) tam giác DEF cân tại D, I là trung điểm của EF suy ra DI là đường trung tuyến đồng thời là đường cao
suy ra DI vuông góc với EF tại I
Xét tam giác DIF vuông tại I suy ra DF2 = DI2+IF2 (Định lý pytago) (8)
Xét tam giác DIN vuông tại N suy ra IN2 = DI2- DN2 (Định lý pytago) (9)
Xét tam giác FIN vuông tại N suy ra IN2 = IF2- NF2 (Định lý pytago) (10)
Cộng vế của (9) và (10) ta được 2 .IN2=DI2- DN2 +IF2- NF2 (11)
Từ (8) suy ra IF2=DF2-DI2 (12)
Thay (12) vào (11) ta được 2 .IN2=DI2- DN2 +DF2-DI2- NF2 =DF2- DN2 - NF2
a) xét tg DEI và DFI
có: DE=DF( GIẢ THUYẾT)
EI=IF(I là trung điểm)
<E=<F(tg DEF cân)
=>DEI=DFI
b
a) xét tg DEI và DFI
có: DE=DF( GIẢ THUYẾT)
EI=IF(I là trung điểm)
<E=<F(tg DEF cân)
=>DEI=DFI
câu b tương tự nha
k mk nha
a: Ta có: ΔDEF cân tại D
mà DI là đường trung tuyến
nên DI là phân giác
b: Xét ΔDMI vuông tại M và ΔDNI vuông tại N có
DI chung
\(\widehat{MDI}=\widehat{NDI}\)
DO đó; ΔDMI=ΔDNI
Suy ra: IM=IN
hay ΔIMN cân tại I
a: Ta có: ΔDEF cân tại D
mà DH là đường cao
nên H là trung điểm của FE
hay HF=HE
b: EF=6cm nên HF=3cm
=>DH=4cm
c: Xét ΔDME và ΔDNF có
DM=DN
\(\widehat{EMD}\) chung
DE=DF
Do đó: ΔDME=ΔDNF
\(\text{#TNam}\)
`a,` Xét Tam giác `HED` và Tam giác `HFD` có
`DE = DF (\text {Tam giác DEF cân tại D})`
\(\widehat{E}=\widehat{F}\) `(\text {Tam giác DEF cân tại D})`
`=> \text {Tam giác HED = Tam giác HDF (ch-gn)}`
`b,` Vì Tam giác `HED =` Tam giác `HFD (a)`
`-> HE = HF (\text {2 cạnh tương ứng})`
Xét Tam giác `HEM` và Tam giác `HFN` có:
`HE = HF (CMT)`
\(\widehat{E}=\widehat{F}\) `(a)`
\(\widehat{EMH}=\widehat{FNH}=90^0\)
`=> \text {Tam giác HEM = Tam giác HFN (ch-gn)}`
`-> EM = FN (\text {2 cạnh tương ứng})`
Ta có: \(\left\{{}\begin{matrix}DE=MD+ME\\DF=ND+NF\end{matrix}\right.\)
Mà `DE = DF, ME = NF`
`-> MD = ND`
Xét Tam giác `DMN: DM = DN (CMT)`
`-> \text {Tam giác DMN cân tại D}`
`->`\(\widehat{DMN}=\widehat{DNM}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `DEF` cân tại `D`
`->`\(\widehat{E}=\widehat{F}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{DMN}=\widehat{E}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {MN // EF (t/c 2 đt' //)}`
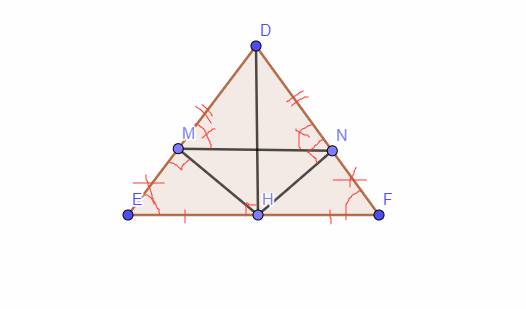
a/ xét /\ DEF cân tại D
=> DE = DF (t/c /\ cân )
DI là trung tuyến
=> DI vuông với FE => DIE = 90* => DIF kề bù với DIE => DIF = 90* (1)
=> I là trung điểm EF
Xét /\ DIF và /\ DIE có :
DIF = DIE (cmt )
DF =DE (cmt)
IF = IE ( cmt )
=> /\ DIE = /\ DIF (c.g.c)
b/ (1) => DIE = DIF = 90*
=> 2 góc này là hai góc vuông
c/ chịu .
a: Xét ΔEHD và ΔEHF có
EH chung
\(\widehat{HED}=\widehat{HEF}\)
ED=EF
Do đó: ΔEHD=ΔEHF
c: Ta có; ΔEHD=ΔEHF
=>HF=HD
mà H nằm giữa D và F
nên H là trung điểm của DF
=>\(HD=\dfrac{DF}{2}=3\left(cm\right)\)
ΔEHD vuông tại H
=>\(EH^2+HD^2=ED^2\)
=>\(EH^2=5^2-3^2=16\)
=>\(EH=\sqrt{16}=4\left(cm\right)\)
