Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Ta có ∆DEF vuông vì D E 2 + D F 2 = F E 2
b, c, Tìm được: DK = 24 5 cm và HK = 32 5 cm
K D E ^ ≈ 36 0 52 ' ; K E D ^ = 35 0 8 '
d, Tìm được DM=3cm, FM=5cm và EM = 3 5 cm
e, f, Ta có: sin D F K ^ = D K D F ; sin D F E ^ = D E E F
=> D K D F = D E E F => ED.DF = DK.EF

a: Xét ΔDEF có \(EF^2=DE^2+DF^2\)
nên ΔDEF vuông tại D

trong \(\Delta DEF\) vuông tại D có
\(DK^2=EK.KF\)(đlý)\(\Rightarrow KF=\dfrac{DK^2}{EK}=\dfrac{6^2}{8}\)=4,5
ta có:EF=EK+KF=8+4,5=12,5
\(DE^2=EF.EK\left(đlý\right)\)=12,5.8=100\(\Rightarrow DE=10\)
\(DF^2=EF.KF\)(đlý)=12,5.4,5=56,25\(\Rightarrow\)DF=7,5

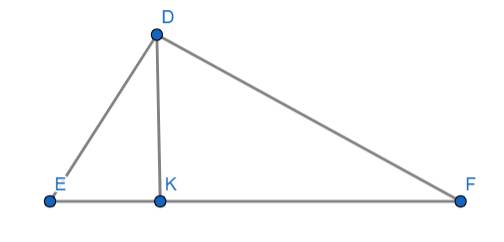
Xét ta có:
\(EF^2=7,5^2=56,25\left(cm\right)\) (1)
Mà: \(DF^2+DE^2=4,5^2+6^2=56,25\left(cm\right)\) (2)
Từ (1) và (2) ta có:
\(EF^2=DE^2+DF^2\)
\(\Rightarrow\Delta DEF\) vuông tại D có đường cao DK
a) Áp dụng hệ thức hai cạnh góc vuông và đường cao ta có:
\(\dfrac{1}{DK^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}\)
\(\Rightarrow DK^2=\dfrac{DE^2DF^2}{DF^2+DF^2}\Rightarrow DK=\sqrt{\dfrac{DE^2DF^2}{DF^2+DE^2}}\)
\(\Rightarrow DK=\sqrt{\dfrac{4,5^2\cdot6^2}{4,5^2+6^2}}=3,6\left(cm\right)\)
b) Áp dụng hệ thức hình chiếu và cạnh góc vuông ta có:
\(\left\{{}\begin{matrix}DE^2=EF\cdot EK\\DF=EF\cdot FK\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}EK=\dfrac{DE^2}{EF}\\FK=\dfrac{DF^2}{EF}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}EK=\dfrac{6^2}{7,5}=4,8\left(cm\right)\\FK=\dfrac{4,5^2}{7,5}=2,7\left(cm\right)\end{matrix}\right.\)
a: Xét ΔDEF có EF^2=DE^2+DF^2
nên ΔDEF vuông tại D
Xét ΔDEF vuông tại D có DK là đường cao
nên DK*FE=DE*DF
=>DE*7,5=27
=>DE=3,6cm
b: ΔDEF vuông tại D có DK là đường cao
nên EK*EF=ED^2
=>EK=6^2/7,5=4,8cm
FK=7,5-4,8=2,7cm
a: Xét ΔDEF có \(EF^2=DE^2+DF^2\)
nên ΔDEF vuông tại D
b: Xét ΔDEF vuông tại D có DK là đường cao
nên \(\left\{{}\begin{matrix}DK\cdot FE=DE\cdot DF\\DF^2=FK\cdot FE\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DK=4.8\left(cm\right)\\FK=6.4\left(cm\right)\end{matrix}\right.\)
cau C va cau D dau ban?